8 minutes
XCTF CRYPTO novice_writeup
这次又是XCTF平台,没错,我又来无聊谈谈解题了
首先先来一张XCTF的首页图片,来开启本次的writeup文章:
xctf首页
这次我们要搞哪些题目的思路呢?这次还是新手区,不过是不一样的新手局,这回盘一盘密码学。
crypto新手区题目
题目数量不变,依然是12道题目:
- base64
- Caesar
- Morse
- 幂数加密
- Railfence
- 不仅仅是Morse
- 混合编码
- easy_RSA
- easychallenge
- 转轮机加密
- Normal_RSA
- esay_ECC
在开始进行密码学的题目问题思路分析的开始之前,首先进行一部分知识的了解。
密码学的CTF题目通常都是以附件形式来进行考察的。不像网页需要进入到平台设定的docker靶机中
CTF中密码学题目目前的趋势是越来越难,而且分值越来越高。密码学的题目往往分为编码题目和密码学题目,而密码学题目又会分为古典密码学题目和现代密码学题目。
密码学早在公元前400多年就已经产生,人类使用密码的历史几乎与使用文字的时间一样长,密码学的发展大致可以分为 3 个阶段: 1949 年之前的古典密码学阶段; 1949 年至 1975 年密码学成为科学的分支; 1976 年以后对称密钥密码算法得到进一步发展,产生了密码学的新方向—公钥密码学。1976 年,W.Diffie 和 M.Hellman 在发表的文章“密码学的新方向”中首次公开提出了公钥密码( Public-key Cryptography) 的概念。公钥密码的提出实现了加密密钥和解密密钥之间的独立,解决了对称密码体制中通信双方必须共享密钥的问题,在密码学界具有划时代的意义。[1]
CTF中的编码题目往往会考察一些常用的编码类型,当然也会出现一些比较偏的编码方式进行编码。
常用的编码方式有:ASCii编码,Base64编码,Bin编码,Hex编码,URL编码以及HTML编码。
CTF中的古典密码学题目可以通过查找相关的密码学算法来了解与密码学相关内容的更多信息,通过网络方式进行解决,或者获取一些灵感。古典密码学经常会考察最基础的凯撒密码,栅栏密码,或者替换密码。这些古典密码学的处理思路和方式都比较相似,而且网络已经有很多处理这些密码的算法工具来进行加密和解密。
CTF中的现代密码学题目主要会考察RSA加密算法,ECC加密算法等经典的现代密码学算法。也会有一些新的加密算法题目,这种题目往往需要进行算法分析,通过加密算法的语法逻辑来设计解密算法通过逆元的思维求出明文。
关于密码学的更多内容,可以访问:http://eol.sicau.edu.cn:8080/ 来了解更多密码学相关的内容。
下面就开始本回的题目!
base64
看到这道题目,猜想这道题目可能是考察base64编码方式的密码学题目
进入道题目页面,看看是否可以得到一点tip:
 base64题目
base64题目
没有什么特别的tip,只是给题目一个情景化的描述,没有太多有用信息的描述。
直接下载附件内容,并打开附件文件进行查看:
 附件文件
附件文件
文件内容有一段字符型文字:Y3liZXJwZWFjZXtXZWxjb21lX3RvX25ld19Xb3JsZCF9
根据题目的内容,尝试使用一下base64进行解码,可以使用在线的解码工具,也可以使用python脚本进行解码。这里编写简单的python脚本进行解码:
# python3 脚本
import base64
cipher='Y3liZXJwZWFjZXtXZWxjb21lX3RvX25ld19Xb3JsZCF9'
plainer= base64.b64decode(cipher)
print(str(plainer,'utf-8'))
# python2 脚本
import base64
cipher='Y3liZXJwZWFjZXtXZWxjb21lX3RvX25ld19Xb3JsZCF9'
plainer= base64.b64decode(cipher)
print(plainer)
然后运行python脚本进行解码:
python base64_decode.py # 这里创建的python2脚本文件名是base64_decode.py
python3 base64_decode3.py # 这里创建的python3脚本文件名是base64_decode3.py
执行命令后查看执行结果

成功拿到flag数据,这道题目是道签到题。
这道题目主要考察base64编码知识,没有什么难度,就是一道签到题目。
Caesar
看到题目,自然就联系到Caesar cipher,翻译成中文就是凯撒密码。
所有解决这道题目的关键就是凯撒密码的密码逻辑了
凯撒密码(英语:Caesar cipher),或称凯撒加密、凯撒变换、变换加密,是一种最简单且最广为人知的加密技术。凯撒密码是一种替换加密技术,明文中的所有字母都在字母表上向后(或向前)按照一个固定数目进行偏移后被替换成密文。例如,当偏移量是3的时候,所有的字母A将被替换成D,B变成E,以此类推。这个加密方法是以罗马共和时期凯撒的名字命名的,据称当年凯撒曾用此方法与其将军们进行联系。[2]
点开题目的页面,看看是否有些有用的信息
 Caesar题目
Caesar题目
从题目描述中依旧获取不到更多的信息,没有太多有用的信息可以帮助解题
直接下载附件并进行查看:
 附件内容
附件内容
附件内容中,只有一段加密文字:oknqdbqmoq{kag_tmhq_xqmdzqp_omqemd_qzodkbfuaz}
根据题目这应该是凯撒加密算法,可以使用在线的工具进行解密,也可以使用python脚本进行解决,这里使用python脚本进行解密:
# python2脚本
dict_list = ['a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z']
cipher = "oknqdbqmoq{kag_tmhq_xqmdzqp_omqemd_qzodkbfuaz}"
for j in range(26):
plainer = ""
for i in cipher:
if i in dict_list:
plainer += dict_list[(dict_list.index(i)-j)%26]
else:
plainer += i
print plainer
# pyhton3脚本
dict_list = ['a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z']
cipher = "oknqdbqmoq{kag_tmhq_xqmdzqp_omqemd_qzodkbfuaz}"
for j in range(26):
plainer = ""
for i in cipher:
if i in dict_list:
plainer += dict_list[(dict_list.index(i)-j)%26]
else:
plainer += i
print(plainer)
这道题目的python2和python3脚本差别不大,虽然密码学的大多数题目还是推荐使用python2进行编写,但是对于使用sagemath的密码学题目,python3还是比较适合。下面运行python脚本:
# python2
python Caesar_decode.py
# python3
python3 Caesar_decode3.py
查看终端显示的运行结果:
 运行结果
运行结果
从运行结果发现:cyberpeace{you_have_learned_caesar_encryption} 应该是有明显含义的解密的文段,很可能是这道题目的flag。尝试进行提交,发现这段数据就是flag数据。
这道题目解决,题目没有什么难度,算是签到题。
题目主要考察凯撒密码的相关知识,非常直接的解密方法,没有什么难度。
Morse
看到题目Morse,自然而然便联想到了摩尔斯电码。这道题目有可能是在考察摩尔斯电码。
点开题目页面,看看题目描述中会有什么有用的信息:
 Morse题目
Morse题目
题目描述依然是大片无用的信息,但是最后提示了提交flag的格式和内容要求。
直接打开附件并进行查看需要进行解密的内容:
 附件内容
附件内容
文件内容非常像bin方式的加密,但是考虑到题目Morse,应该是Morse电码方式的加密
首先,需要了解什么摩尔斯电码:
摩尔斯电码(英语:Morse code)是一种时通时断的信号代码,通过不同的排列顺序来表达不同的英文字母、数字和标点符号。是由美国人艾尔菲德·维尔与萨缪尔·摩尔斯在1836年发明。[3]
摩尔斯电码是一种早期的数字化通信形式,但是它不同于现代只使用0和1两种状态的二进制代码,它的代码包括五种:
- 点(·):1
- 划(-):111
- 字符内部的停顿(在点和划之间):0
- 字符之间的停顿:000
- 单词之间的停顿:0000000
根据摩尔斯电码的知识点,这道题目可以使用在线工具进行解密,也可以使用python脚本进行解密。这里使用python脚本进行解密:
这里的密文文段和摩尔斯代码的文段不太一致,需要进行一下代换。这里使用 1 代表 - ,0 代表 ·
来进行摩尔斯电码的解密算法的设计和编写。
# python2脚本
dict_list = {
'01':'a',
'1000':'b',
'1010':'c',
'100':'d',
'0':'e',
'0010':'f',
'110':'g',
'0000':'h',
'00':'i',
'0111':'j',
'101':'k',
'0100':'l',
'11':'m',
'10':'n',
'111':'o',
'0110':'p',
'1101':'q',
'010':'r',
'000':'s',
'1':'t',
'001':'u',
'0001':'v',
'011':'w',
'1001':'x',
'1011':'y',
'1100':'z'
}
cipher="11 111 010 000 0 1010 111 100 0 00 000 000 111 00 10 1 0 010 0 000 1 00 10 110"
plainer=""
cipher_arr = cipher.split(" ")
for i in cipher_arr:
plainer += dict_list[i]
print plainer
# python3脚本
dict_list = {
'01':'a',
'1000':'b',
'1010':'c',
'100':'d',
'0':'e',
'0010':'f',
'110':'g',
'0000':'h',
'00':'i',
'0111':'j',
'101':'k',
'0100':'l',
'11':'m',
'10':'n',
'111':'o',
'0110':'p',
'1101':'q',
'010':'r',
'000':'s',
'1':'t',
'001':'u',
'0001':'v',
'011':'w',
'1001':'x',
'1011':'y',
'1100':'z'
}
cipher="11 111 010 000 0 1010 111 100 0 00 000 000 111 00 10 1 0 010 0 000 1 00 10 110"
plainer=""
cipher_arr = cipher.split(" ")
for i in cipher_arr:
plainer += dict_list[i]
print(plainer)
这道题目的python2和python3的求解脚本差别也不是非常大,执行脚本后直接查看执行结果:
 执行结果
执行结果
发现执行结果是一句有意义的句子,应该就是flag数据了。然后再利用题目描述所说的信息对执行出来的flag数据进行个加帽处理:cyberpeace{morsecodeissointeresting}
题目解决,题目也是签到题,没有什么难度。
题目主要考察了摩尔斯电码的解密方法,以及摩尔斯电码相关知识,签到题。
幂数加密
看到题目的时候有些懵逼,本菜鸡不太了解什么的是幂数加密,于是只能求助一下搜索引擎。
 二进制幂数加密-百度百科
二进制幂数加密-百度百科
好像是一个加密方法,这种加密方法大致逻辑是:
- 将明文对应字母序列
- 对字母序列进行处理加密
- 使用间隔符进行间隔
- 获得密文
现在知道这种加密方法,点开题目的描述看看是否可以获取到更多的信息
 幂数加密题目
幂数加密题目
题目描述中仅仅告诉了需要提交的flag格式,和flag数据类型。题目描述的其他信息都是无用的信息。
将附件下载下来并查看附件中的密文信息内容:
 附件资料
附件资料
发现密文数据不太对劲呀,二进制幂数加密的数据都是01234的形式,这个密文的形式是01248的形式
于是作为菜鸡的我只能去再次求助于搜索引擎了,查到了云影密码:
01248云影密码
原理:有1,2,4,8这四个数字,可以通过加法来用这四个数字表示0-9中的任何一个数字,列如0=28, 也就是0=2+8,同理7=124, 9=18。这样之后再用1-26来表示26个英文字母,就有了密文与明文之间的对应关系。引入0来作为间隔,以免出现混乱。所以云影密码又叫“01248密码”。[4]
看来密文是云影密码没错了,由于云影密码是比较少见的密码,而是加密逻辑比较简单,网络上几乎没有什么可用的在线工具。这道题目可以使用手工解密,也可以使用python脚本进行解密。这里使用python脚本进行解密:
# python2
dict_list = ['a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z']
cipher="8842101220480224404014224202480122"
cipher_array = cipher.split("0")
cipher_arr = []
flag = ""
for i in cipher_array:
k = 0
for j in range(len(i)):
k += int(i[j])
cipher_arr.append(k)
for m in cipher_arr:
flag += dict_list[m-1]
print flag
# python3
dict_list = ['a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z']
cipher="8842101220480224404014224202480122"
cipher_array = cipher.split("0")
cipher_arr = []
flag = ""
for i in cipher_array:
k = 0
for j in range(len(i)):
k += int(i[j])
cipher_arr.append(k)
for m in cipher_arr:
flag += dict_list[m-1]
print(flag)
执行python脚本并查看终端输出的结果:
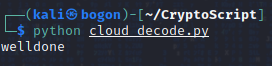
获取到明文,然后对明文加个flag数据形式的帽子并进行字母大写:cyberpeace{WELLDONE}
这道题目解决,题目属于签到题,没有什么难度
这道题目主要考察幂数加密的知识,(云影密码的设计逻辑其实和幂数加密相似,只是在设计过程进行了修改。)题目难度比较低·,签到题。
Railfence
看到题目大致知道考察的是什么密码的加密算法了,题目是栅栏,应该就是栅栏密码的密码知识考察
什么是栅栏密码呢?
所谓栅栏密码,就是把要加密的明文分成N个一组,然后把每组的第1个字连起来,形成一段无规律的话。 不过栅栏密码本身有一个潜规则,就是组成栅栏的字母一般不会太多。(一般不超过30个,也就是一、两句话)。加密原理:
- 把将要传递的信息中的字母交替排成上下两行。
- 再将下面一行字母排在上面一行的后边,从而形成一段密码。[5]
栅栏密码大致就是一种分组密码的一种密码算法,便于更好理解栅栏密码,这里有一个例子:
明文:THE LONGEST DAY MUST HAVE AN END5
加密:
- 把将要传递的信息中的字母交替排成上下两行。 T E O G S D Y U T A E N N H L N E T A M S H V A E D
- 密文:将下面一行字母排在上面一行的后边。 TEOGSDYUTAENN HLNETAMSHVAED
解密:
先将密文分为两行
T E O G S D Y U T A E N N
H L N E T A M S H V A E D
再按上下上下的顺序组合成一句话明文:
THE LONGEST DAY MUST HAVE AN EN
现在知识也大致了解了,点开题目揭开这道题目的真实面目吧!
 Railfence题目
Railfence题目
题目描述中也暗示了是栅栏密码的信息
于是直接下载附件,看看附件中的描述内容密文究竟是啥样:
 附件内容
附件内容
密文形式看样子像是解密出来直接就是flag数据。
这道题目可以使用在线工具进行解密,也可以使用python脚本进行解密。这里还是一如既往,使用python脚本进行解密:(这道题目比较狗,是W型的栅栏密码解密)
栅栏密码有两种类型:一种是传统型栅栏密码,一种是W型栅栏密码,W型栅栏密码比较复杂。
传统型栅栏密码脚本:
def decrype(cipher,key):
cipher_len = len(cipher)
if cipher_len%key == 0:
key = cipher_len / key
else:
key = cipher_len / key + 1
result = {x:'' for x in range(key)}
for i in range(cipher_len):
a = i%key;
result.update({a:result[a]+cipher[i]})
plainer=""
for i in range(key):
plainer = plainer + result[i]
print plainer
cipher="TEOGSDYUTAENNHLNETAMSHVAED"
for n in range(2,10):
decrype(cipher,n)
W型栅栏密码脚本:
def fence(lst, numrails):
fence = [[None] * len(lst) for n in range(numrails)]
rails =list(range(numrails - 1))+ list(range(numrails - 1, 0, -1))
for n, x in enumerate(lst):
fence[rails[n % len(rails)]][n] = x
return [c for rail in fence for c in rail if c is not None]
def encode(text, n):
return ''.join(fence(text, n))
def decode(text, n):
rng = range(len(text))
pos = fence(rng, n)
return ''.join(text[pos.index(n)] for n in rng)
z = "ccehgyaefnpeoobe{lcirg}epriec_ora_g"
for i in range(2,10):
y = decode(z,i)
print(y)
这道题目是W型的栅栏密码,这里使用W型栅栏密码的脚本进行破解:
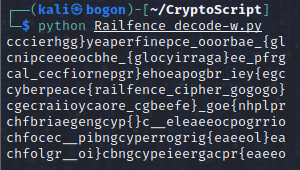
成功跑出flag数据:cyberpeace{railfence_cipher_gogogo}
题目解决,这道题目属于简单题目
题目主要考察对栅栏密码的知识全面性考察,如果知识不全面可能会有一点绕,不容易解出。难度算是简单题目。
不仅仅是Morse
看题目应该知道这道题目不是非常简单的样子,应该是一个复合加密的题目,就是涉及多种加密算法的加密。
点开题目页面,希望可以获取到更多关于题目的tip:
 题目页面
题目页面
题目描述中有两个重要的tip信息:flag的数据格式和flag是一种食物的单词。对于解题有主要作用的是flag数据是一种食物的单词。
下面打开附件,进行解密:
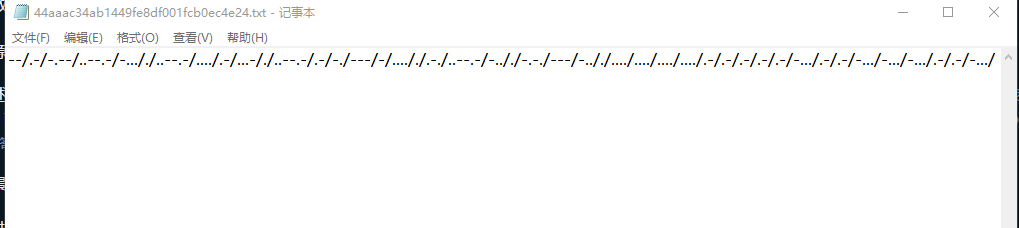 附件内容
附件内容
看来是一个摩尔斯电码的加密:
--/.-/-.--/..--.-/-..././..--.-/..../.-/...-/./..--.-/.-/-./---/-/...././.-./..--.-/-.././-.-./---/-.././..../..../..../..../.-/.-/.-/.-/.-/-.../.-/.-/-.../-.../-.../.-/.-/-.../-.../.-/.-/.-/.-/.-/.-/.-/.-/-.../.-/.-/-.../.-/-.../.-/.-/.-/.-/.-/.-/.-/-.../-.../.-/-.../.-/.-/.-/-.../-.../.-/.-/.-/-.../-.../.-/.-/-.../.-/.-/.-/.-/-.../.-/-.../.-/.-/-.../.-/.-/.-/-.../-.../.-/-.../.-/.-/.-/-.../.-/.-/.-/-.../.-/.-/-.../.-/-.../-.../.-/.-/-.../-.../-.../.-/-.../.-/.-/.-/-.../.-/-.../.-/-.../-.../.-/.-/.-/-.../-.../.-/-.../.-/.-/.-/-.../.-/.-/-.../.-/.-/-.../.-/.-/.-/.-/-.../-.../.-/-.../-.../.-/.-/-.../-.../.-/.-/-.../.-/.-/-.../.-/.-/.-/-.../.-/.-/-.../.-/.-/-.../.-/.-/-.../.-/-.../.-/.-/-.../-.../.-/-.../.-/.-/.-/.-/-.../-.../.-/-.../.-/.-/-.../-.../.-
首先先编写一个摩尔斯电码的解密脚本:(当然也可以使用在线的摩尔斯电码解密工具进行解密)
# python2
dict_list = {
'.-':'a',
'-...':'b',
'-.-.':'c',
'-..':'d',
'.':'e',
'..-.':'f',
'--.':'g',
'....':'h',
'..':'i',
'.---':'j',
'-.-':'k',
'.-..':'l',
'--':'m',
'-.':'n',
'---':'o',
'.--.':'p',
'--.-':'q',
'.-.':'r',
'...':'s',
'-':'t',
'..-':'u',
'...-':'v',
'.--':'w',
'-..-':'x',
'-.--':'y',
'--..':'z',
'..--.-':'_'
}
cipher = "--/.-/-.--/..--.-/-..././..--.-/..../.-/...-/./..--.-/.-/-./---/-/...././.-./..--.-/-.././-.-./---/-.././..../..../..../..../.-/.-/.-/.-/.-/-.../.-/.-/-.../-.../-.../.-/.-/-.../-.../.-/.-/.-/.-/.-/.-/.-/.-/-.../.-/.-/-.../.-/-.../.-/.-/.-/.-/.-/.-/.-/-.../-.../.-/-.../.-/.-/.-/-.../-.../.-/.-/.-/-.../-.../.-/.-/-.../.-/.-/.-/.-/-.../.-/-.../.-/.-/-.../.-/.-/.-/-.../-.../.-/-.../.-/.-/.-/-.../.-/.-/.-/-.../.-/.-/-.../.-/-.../-.../.-/.-/-.../-.../-.../.-/-.../.-/.-/.-/-.../.-/-.../.-/-.../-.../.-/.-/.-/-.../-.../.-/-.../.-/.-/.-/-.../.-/.-/-.../.-/.-/-.../.-/.-/.-/.-/-.../-.../.-/-.../-.../.-/.-/-.../-.../.-/.-/-.../.-/.-/-.../.-/.-/.-/-.../.-/.-/-.../.-/.-/-.../.-/.-/-.../.-/-.../.-/.-/-.../-.../.-/-.../.-/.-/.-/.-/-.../-.../.-/-.../.-/.-/-.../-.../.-"
plainer = ""
cipher_arr = cipher.split('/')
for i in cipher_arr:
plainer += dict_list[i]
print plainer
执行编写好的python脚本,并查看终端的返回结果:

获得一段解密后的文段:
may_be_have_another_decodehhhhaaaaabaabbbaabbaaaaaaaabaababaaaaaaabbabaaabbaaabbaabaaaababaabaaabbabaaabaaabaababbaabbbabaaabababbaaabbabaaabaabaabaaaabbabbaabbaabaabaaabaabaabaababaabbabaaaabbabaabba
仔细看看文段,好像出题人想要我们去解密后面那段ab组成的密文
那段密文形式没有见过,于是本菜鸡又去求助搜索引擎了。搜索发现是培根密码,正好于tip相对应了。那什么是培根密码呢?
培根密码,又名倍康尼密码(英语:Bacon’s cipher)是由法兰西斯·培根发明的一种隐写术。
加密时,明文中的每个字母都会转换成一组五个英文字母。其转换依靠下表:
a AAAAA g AABBA n ABBAA t BAABA
b AAAAB h AABBB o ABBAB u-v BAABB
c AAABA i-j ABAAA p ABBBA w BABAA
d AAABB k ABAAB q ABBBB x BABAB
e AABAA l ABABA r BAAAA y BABBA
f AABAB m ABABB s BAAAB z BABBB
这只是一款最常用的加密表,有另外一款将每种字母配以不同的字母组予以转换,即I与J、U与V皆有不同编号。
加密者需使用两种不同字体,分别代表A和B。准备好一篇包含相同AB字数的假信息后,按照密文格式化假信息,即依密文中每个字母是A还是B分别套用两种字体。
解密时,将上述方法倒转。所有字体一转回A,字体二转回B,以后再按上表拼回字母。
法兰西斯·培根另外准备了一种方法,其将大小写分别看作A与B,可用于无法使用不同字体的场合(例如只能处理纯文本时)。但这样比起字体不同更容易被看出来,而且和语言对大小写的要求也不太兼容。
培根密码本质上是将二进制信息通过样式的区别,加在了正常书写之上。培根密码所包含的信息可以和用于承载其的文章完全无关。[6]
将摩尔斯电码解密出来的文段的后半部分取出作为密文,即:
aaaaabaabbbaabbaaaaaaaabaababaaaaaaabbabaaabbaaabbaabaaaababaabaaabbabaaabaaabaababbaabbbabaaabababbaaabbabaaabaabaabaaaabbabbaabbaabaabaaabaabaabaababaabbabaaaabbabaabba
可以使用网上的培根密码工具进行解密也可以使用python脚本进行解密,这里使用python脚本进行解密:
# python2
dict_list={
'aaaaa':'a',
'aaaab':'b',
'aaaba':'c',
'aaabb':'d',
'aabaa':'e',
'aabab':'f',
'aabba':'g',
'aabbb':'h',
'abaaa':'i',
'abaab':'j',
'ababa':'k',
'ababb':'l',
'abbaa':'m',
'abbab':'n',
'abbba':'o',
'abbbb':'p',
'baaaa':'q',
'baaab':'r',
'baaba':'s',
'baabb':'t',
'babaa':'u',
'babab':'v',
'babba':'w',
'babbb':'x',
'bbaaa':'y',
'bbaab':'z'
}
cipher = "aaaaabaabbbaabbaaaaaaaabaababaaaaaaabbabaaabbaaabbaabaaaababaabaaabbabaaabaaabaababbaabbbabaaabababbaaabbabaaabaabaabaaaabbabbaabbaabaabaaabaabaabaababaabbabaaaabbabaabba"
plainer = ""
cipher_arr = []
[cipher_arr.append(cipher[i:i+5]) for i in range(0,len(cipher),5)]
for i in cipher_arr:
plainer =plainer+dict_list[i]
print plainer
执行python脚本,并查看终端返回的结果:
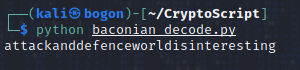
看来输出的结果应该就是未成熟的flag数据:attackanddefenceworldisinteresting
对这个数据进行加帽处理:cyberpeace{attackanddefenceworldisinteresting}
flag数据成功拿到
这道题目主要考察古典密码学的替换加密算法知识,难度上应该算是简单题,思路也是比较流畅的。
混合编码
看到题目,这道题应该是考察编码相关的知识的内容
点开题目页面,看看能得到什么关键信息:
 混合编码题目
混合编码题目
题目描述中就有一个关键信息,就是题目的要求提交的flag数据格式信息,没有其他关键性的信息了
下载附件并打开查看密文:
 附件内容
附件内容
附件中的密文内容看样子像是base64编码格式的:
JiM3NjsmIzEyMjsmIzY5OyYjMTIwOyYjNzk7JiM4MzsmIzU2OyYjMTIwOyYjNzc7JiM2ODsmIzY5OyYjMTE4OyYjNzc7JiM4NDsmIzY1OyYjNTI7JiM3NjsmIzEyMjsmIzEwNzsmIzUzOyYjNzY7JiMxMjI7JiM2OTsmIzEyMDsmIzc3OyYjODM7JiM1NjsmIzEyMDsmIzc3OyYjNjg7JiMxMDc7JiMxMTg7JiM3NzsmIzg0OyYjNjU7JiMxMjA7JiM3NjsmIzEyMjsmIzY5OyYjMTIwOyYjNzg7JiMxMDU7JiM1NjsmIzEyMDsmIzc3OyYjODQ7JiM2OTsmIzExODsmIzc5OyYjODQ7JiM5OTsmIzExODsmIzc3OyYjODQ7JiM2OTsmIzUwOyYjNzY7JiMxMjI7JiM2OTsmIzEyMDsmIzc4OyYjMTA1OyYjNTY7JiM1MzsmIzc4OyYjMTIxOyYjNTY7JiM1MzsmIzc5OyYjODM7JiM1NjsmIzEyMDsmIzc3OyYjNjg7JiM5OTsmIzExODsmIzc5OyYjODQ7JiM5OTsmIzExODsmIzc3OyYjODQ7JiM2OTsmIzExOTsmIzc2OyYjMTIyOyYjNjk7JiMxMTk7JiM3NzsmIzY3OyYjNTY7JiMxMjA7JiM3NzsmIzY4OyYjNjU7JiMxMTg7JiM3NzsmIzg0OyYjNjU7JiMxMjA7JiM3NjsmIzEyMjsmIzY5OyYjMTE5OyYjNzc7JiMxMDU7JiM1NjsmIzEyMDsmIzc3OyYjNjg7JiM2OTsmIzExODsmIzc3OyYjODQ7JiM2OTsmIzExOTsmIzc2OyYjMTIyOyYjMTA3OyYjNTM7JiM3NjsmIzEyMjsmIzY5OyYjMTE5OyYjNzc7JiM4MzsmIzU2OyYjMTIwOyYjNzc7JiM4NDsmIzEwNzsmIzExODsmIzc3OyYjODQ7JiM2OTsmIzEyMDsmIzc2OyYjMTIyOyYjNjk7JiMxMjA7JiM3ODsmIzY3OyYjNTY7JiMxMjA7JiM3NzsmIzY4OyYjMTAzOyYjMTE4OyYjNzc7JiM4NDsmIzY1OyYjMTE5Ow==
使用在base64关卡中的python脚本进行base64解密(当然也可以使用在线工具进行base64解密)

接出来的数据好像又是一种编码格式:
LzExOS8xMDEvMTA4Lzk5LzExMS8xMDkvMTAxLzExNi8xMTEvOTcvMTE2LzExNi85Ny85OS8xMDcvOTcvMTEwLzEwMC8xMDAvMTAxLzEwMi8xMDEvMTEwLzk5LzEwMS8xMTkvMTExLzExNC8xMDgvMTAw
看样子应该是ascii编码格式,可以使用在线的ascii编码工具进行解密,也可使用python脚本进行解密,一如既往,这里使用python脚本进行解密:
# python2
cipher="LzExOS8xMDEvMTA4Lzk5LzExMS8xMDkvMTAxLzExNi8xMTEvOTcvMTE2LzExNi85Ny85OS8xMDcvOTcvMTEwLzEwMC8xMDAvMTAxLzEwMi8xMDEvMTEwLzk5LzEwMS8xMTkvMTExLzExNC8xMDgvMTAw"
plainer=""
cipher_arr = cipher[2:-1].split(';&#')
for i in cipher_arr:
plainer += chr(int(i))
print plainer
执行编写好的python代码并查看终端输出情况:

输出的解密信息像是base64格式的编码:
LzExOS8xMDEvMTA4Lzk5LzExMS8xMDkvMTAxLzExNi8xMTEvOTcvMTE2LzExNi85Ny85OS8xMDcvOTcvMTEwLzEwMC8xMDAvMTAxLzEwMi8xMDEvMTEwLzk5LzEwMS8xMTkvMTExLzExNC8xMDgvMTAw
可以再使用一次base64解码的python脚本进行base64解码(也可以使用在线base64工具进行解码):

解码后又是一段ascii的编码格式,这里还是编写一个ascii解码的python脚本:
# python2
cipher = "/119/101/108/99/111/109/101/116/111/97/116/116/97/99/107/97/110/100/100/101/102/101/110/99/101/119/111/114/108/100"
plainer = ""
cipher_arr = cipher[1:].split('/')
for i in cipher_arr:
plainer += chr(int(i))
print plainer
执行编写好的python代码并查看终端输出的结果:
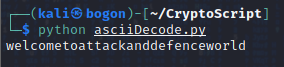
解码出来的数据应该就是flag数据:welcometoattackanddefenceworld
根据题目要求,需要对这个flag数据进行加帽处理:cyberpeace{welcometoattackanddefenceworld}
题目解决,题目属于简单题目,思路就是反复套娃操作:base64->ASCII->base64->ASCII
题目主要考察对编码数据的识别和基本编码方式的解决,简单题。
easy_RSA
看题目,这应该是考察到ctf中密码学的核心模块,也就是现代密码学的部分,RSA加密算法。
什么是RSA加密算法?
RSA加密算法是一种非对称加密算法,在公开密钥加密和电子商业中被广泛使用。RSA是由罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)在1977年一起提出的。当时他们三人都在麻省理工学院工作。RSA 就是他们三人姓氏开头字母拼在一起组成的。
对极大整数做因数分解的难度决定了 RSA 算法的可靠性。换言之,对一极大整数做因数分解愈困难,RSA 算法愈可靠。假如有人找到一种快速因数分解的算法的话,那么用 RSA 加密的信息的可靠性就会极度下降。但找到这样的算法的可能性是非常小的。今天只有短的 RSA 钥匙才可能被强力方式破解。到目前为止,世界上还没有任何可靠的攻击RSA算法的方式。只要其钥匙的长度足够长,用RSA加密的信息实际上是不能被破解的。[7]
RSA是现在密码学的一个典型代表,加密过程不像古典密码学中的密码那么简单,加密过程是非常复杂的。RSA加密算法的安全性也是相当高的。
RSA算法
密钥生成的步骤 [8]
我们通过一个例子,来理解RSA算法。假设爱丽丝要与鲍勃进行加密通信,她该怎么生成公钥和私钥呢?
第一步,随机选择两个不相等的质数p和q。
爱丽丝选择了61和53。(实际应用中,这两个质数越大,就越难破解。)
第二步,计算p和q的乘积n。
爱丽丝就把61和53相乘。
$$ n = 61×53 = 3233 $$
n的长度就是密钥长度。3233写成二进制是110010100001,一共有12位,所以这个密钥就是12位。实际应用中,RSA密钥一般是1024位,重要场合则为2048位。
第三步,计算n的欧拉函数φ(n)。
n是质数,则 φ(n)=n-1 $$ n = p_1 × p_2 $$
$$ φ(n) = φ(p_1 \cdot p_2) = φ(p_1)\cdot φ(p_1) $$
$$ => φ(n) = (p-1)(q-1) $$
爱丽丝算出φ(3233)等于60×52,即3120。
第四步,随机选择一个整数e,条件是1< e < φ(n),且e与φ(n) 互质。
爱丽丝就在1到3120之间,随机选择了17。(实际应用中,常常选择65537。)
第五步,计算e对于φ(n)的模反元素d。
所谓”模反元素”就是指有一个整数d,可以使得ed被φ(n)除的余数为1。
$$ ed ≡ 1 (mod φ(n)) $$
这个式子等价于
$$ ed - 1 = kφ(n) $$
于是,找到模反元素d,实质上就是对下面这个二元一次方程求解。(-k = y)
$$ ex + φ(n)y = 1 $$
已知 e=17, φ(n)=3120,
$$ 17x + 3120y = 1 $$
这个方程可以用“扩展欧几里得算法”(又叫辗转相除法)求解,此处省略具体过程。总之,爱丽丝算出一组整数解为 (x,y)=(2753,-15),即 d=2753。
至此所有计算完成。
第六步,将n和e封装成公钥,n和d封装成私钥。
在爱丽丝的例子中,n=3233,e=17,d=2753,所以公钥就是 (3233,17),私钥就是(3233, 2753)。
实际应用中,公钥和私钥的数据都采用ASN.1格式表达。
这些RSA加密算法的流程和重要的几个参数是解决RSA算法密码学题目的核心,只有清晰地了解RSA加密算法的每个细节,面对RSA题目才能胸有成竹、游刃有余。
点开题目,看看题目描述能给出哪些提示吧:
 easy_RSA
easy_RSA
题目中只有提交格式的提示,除此之外,都是描述性的信息,但是对解题没有太多作用。
下载附件,直接查看附件中的信息:
 附件内容
附件内容
这道题目应该是简单的计算,即根据RSA设计的算法过程进行逆向计算。这道题目可以使用rsatool工具进行直接求解,本菜鸡还是编写一个python脚本进行求解吧:(此脚本只能针对简单问题)
# python2
p=473398607161
q=4511491e=17
pn=(p-1)*(q-1)
flag=(pn+1)/e
print flag
执行编写的脚本,查看终端输出的结果:
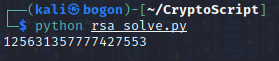
这段输出的数据应该就是flag数据:125631357777427553
给这段flag数据加个帽子:cyberpeace{125631357777427553}
这道题目是RSA题目中的签到题,难度非常低,思路也非常简单
题目主要考察RSA加密算法的过程,签到题。
easychallenge
这道题的题目似乎看不出什么门路来,于是只能点开题目描述的页面:
 easychallenge题目
easychallenge题目
这道题目应该是在说程序方面的问题,题目描述也得到不了太多有用的信息,于是下载附件来获取到这道题目的真实面目:

发现附件是一个python的一个可以执行的文件,查看文件的属性:
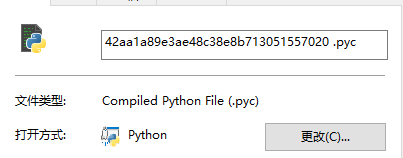
发现是一个pyc文件,本菜鸡不知道什么是pyc文件,于是通过互联网的搜索引擎求助一波:
pyc是一种二进制文件,是由Python文件经过编译后所生成的文件,它是一种byte code,Python文件变成pyc文件后,加载的速度有所提高,而且pyc还是一种跨平台的字节码,由python的虚拟机来执行的,就类似于JAVA或者.NET的虚拟机的概念。pyc的内容与python的版本是相关的,不同版本编译后的pyc文件是不同的,例如2.5版本编译的是pyc文件,而2.4版本编译的python是无法执行的。[9]
pyc文件是py文件经过编译的文件格式,文件内容是一种可执行字节码,尝试执行一下这个文件:

发现需要执行一下这个文件,需要输入flag数据,看来flag数据很可能就在这个文件内部。这里就需要进行反编译,即把pyc文件打回原形。通过互联网的搜索引擎查询到python内置了一个uncompyle模块可以进行pyc反编译。
于是可以使用pip install uncompyle 命令安装一下uncompyle。
在命令行中执行:uncompyle6 -o test.py '.\42aa1a89e3ae48c38e8b713051557020 (1).pyc'
文件应该成功输出成了一个test.py文件。
通过代码编辑器,查看到这个文件的源代码:
# uncompyle6 version 3.7.4
# Python bytecode 2.7 (62211)
# Decompiled from: Python 3.8.6 (tags/v3.8.6:db45529, Sep 23 2020, 15:52:53) [MSC v.1927 64 bit (AMD64)]
# Embedded file name: ans.py
# Compiled at: 2018-08-09 11:29:44
import base64
def encode1(ans):
s = ''
for i in ans:
x = ord(i) ^ 36
x = x + 25
s += chr(x)
return s
def encode2(ans):
s = ''
for i in ans:
x = ord(i) + 36
x = x ^ 36
s += chr(x)
return s
def encode3(ans):
return base64.b32encode(ans)
flag = ' '
print 'Please Input your flag:'
flag = raw_input()
final = 'UC7KOWVXWVNKNIC2XCXKHKK2W5NLBKNOUOSK3LNNVWW3E==='
if encode3(encode2(encode1(flag))) == final:
print 'correct'
else:
print 'wrong'
看到文件源代码,发现flag数据是进行三次加密的:
- 异或处理->加数值chuli->ASCII编码
- 加数值处理->异或处理->ASCII编码
- base32编码处理
我们可以根据这个代码逻辑逆向设计一个加密算法脚本来解决:
# python2
import base64
def decode1(ans):
return base64.b32decode(ans)
def decode2(ans):
s=''
for i in ans:
x = ord(i) ^ 36
x = x -36
s += chr(x)
return s
def decode3(ans):
s=''
for i in ans:
x = ord(i)-25
x = x ^ 36
s += chr(x)
return s
cipher = "UC7KOWVXWVNKNIC2XCXKHKK2W5NLBKNOUOSK3LNNVWW3E==="
plainer = decode3(decode2(decode1(cipher)))
print plainer
执行一下编写好的代码,查看终端输出的结果:
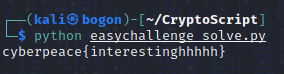
看输出结果,应该是flag数据没错了。
再次执行以下pyc程序验证一下:

看来是没错了,成功获取这道题目的flag数据:cyberpeace{interestinghhhhh}
这道题目的难度上也是简单题,思路也是比较流畅的。
题目主要考察pyc文件的反编译,以及编码和密码学的一些简单理论。简单题。
转轮机加密
看到题目有些懵懵的,本菜鸡不知道啥是转轮机加密,于是只能求助一下搜索引擎来获取与转轮机加密相关的更多信息:
转轮机是古典加密方法的集大成者,二战时轴心国普遍应用了该技术,可惜惨遭盟军攻破,德日还蒙在鼓里,一定程度上改变了最终的战局。
转轮机的原理概括起来就是循环置换的多表代换技术,尤其是多筒转轮机,可重复使用数以万计的字母替换表。
以三筒转轮机为例:

有三个可以独立旋转的圆筒,每个圆筒内部有26个输入引脚和26个输出引脚,内部连线使得输入与输出唯一连接。
每按一下输入键(旋转键),快速转子旋转一个引脚,当快速转子转满一轮(循环归位)时,带动中速转子旋转一个引脚,以此类推,类似钟表的秒分时。
今天,转轮机的意义在于它曾经给目前最广泛使用的密码–数据加密标准DES指明了方向。[10]
转轮机加密是一种古典密码学的一种加密方法,应该是古典密码学的分组密码
加密过程大致是:
明文->分组处理(类似于栅栏密码处理方式)->文段内容位移+密文->多文段顺序重排+密钥->密文组
下面点开题目描述,看看可以得到什么信息:
 转轮机加密题目
转轮机加密题目
根据题目描述的信息,可以获得以下几点提示:
- 二战
- 托马斯·杰斐逊
- flag格式
下面下载附件,并进行查看:
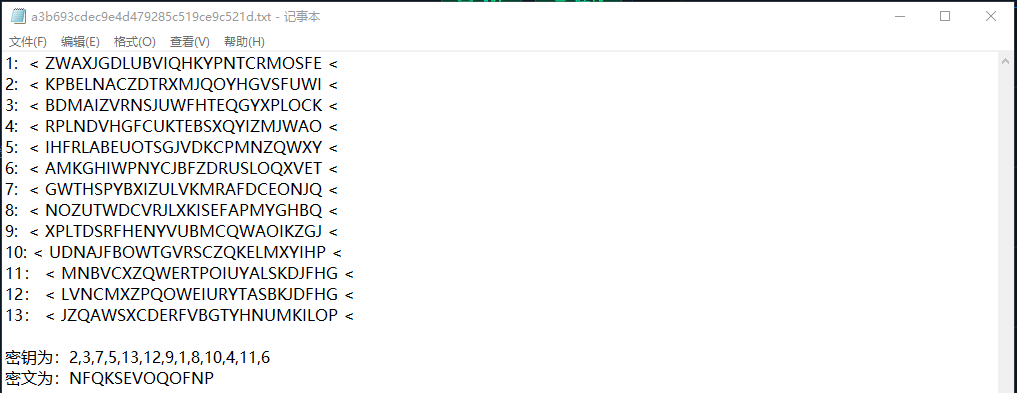 附件内容
附件内容
要想获取到flag数据,应该就需要对附件内容的数据进行机密,这里编写一个python脚本来解密:
# python2
dict_list = {
'1':'ZWAXJGDLUBVIQHKYPNTCRMOSFE', '2':'KPBELNACZDTRXMJQOYHGVSFUWI', '3':'BDMAIZVRNSJUWFHTEQGYXPLOCK', '4':'RPLNDVHGFCUKTEBSXQYIZMJWAO', '5':'IHFRLABEUOTSGJVDKCPMNZQWXY', '6':'AMKGHIWPNYCJBFZDRUSLOQXVET', '7':'GWTHSPYBXIZULVKMRAFDCEONJQ', '8':'NOZUTWDCVRJLXKISEFAPMYGHBQ', '9':'XPLTDSRFHENYVUBMCQWAOIKZGJ', '10':'UDNAJFBOWTGVRSCZQKELMXYIHP', '11':'MNBVCXZQWERTPOIUYALSKDJFHG', '12':'LVNCMXZPQOWEIURYTASBKJDFHG', '13':'JZQAWSXCDERFVBGTYHNUMKILOP'
}
key=[2,3,7,5,13,12,9,1,8,10,4,11,6]
cipher="NFQKSEVOQOFNP"
cipher_arr=[]
plainer_arr=[]
plainer_list=[]
index = 0
for i in key:
cipher_arr.append(dict_list[str(i)])
for j in cipher_arr:
location = j.index(cipher[index])
str_get = j[location:] + j[:location]
plainer_arr.append(str_get)
index += 1
for i in range(len(plainer_arr[0])):
str_get=""
for j in plainer_arr:
str_get += j[i]
print str_get.lower()
执行刚刚编写好的python脚本,并在终端命令行中查看执行结果:
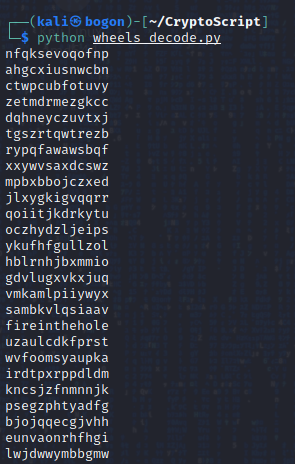
得到了一个明文的列表:
nfqksevoqofnpahgcxiusnwcbnctwpcubfotuvyzetmdrmezgkccdqhneyczuvtxjtgszrtqwtrezbrypqfawawsbqfxxywvsaxdcswzmpbxbbojczxedjlxygkigvqqrrqoiitjkdrkytuoczhydzljeipsykufhfgullzolhblrnhjbxmmiogdvlugxvkxjuqvmkamlpiiywyxsambkvlqsiaavfireintheholeuzaulcdkfprstwvfoomsyaupkairdtpxrppdldmkncsjzfnmnnjkpsegzphtyadfgbjojqqecgjvhheunvaonrhfhgilwjdwwymbbgmw
列表中存在明文,这时候需要看看题目描述的3个tip:
- 二战
- 托马斯·杰斐逊
- flag格式
由于转轮机加密是托马斯·杰斐逊发明的,因而tip2已经使用,tip3是要在提交的时候使用,这时候还有一个tip1,二战。找一下明文列表中是否有与二战相关的文段。
发现文段:fireinthehole 与二战相关,这个明文段应该就是flag数据了。
根据题目描述的flag数据要求,fireinthehole就是正确的flag数据了。
题目解决,题目的思路也是比较流畅简单的,难度上算是简单题。
题目主要考察的是古典密码学中的转轮机加密,简单题。
Normal_RSA
看到题目,感觉这道题目应该不简单,明显的一道RSA加密算法题目,估计也是考察RSA加密算法相关知识的题目。
直接点开题目描述,看看可以获取到什么有用的tip
 Normal_RSA题目
Normal_RSA题目
根据题目描述,这道题目应该是需要使用到工具的。RSA加密算法题目通常会使用到openssl,rsatool,factordb,sagemath工具进行rsa的公钥私钥的运算。
下载附件,查看附件有什么东西吧:
 附件
附件
附件个压缩文件,我们对压缩文件进行解压获得一个文件夹:

打开这个文件夹:
 文件夹内容
文件夹内容
发现有两个文件,一个是公钥,一个是密文。pem格式的文件应该是openssl的一种文件格式

这里使用openssl来获取到公钥文件的e和n,使用openssl的rsa功能之前可以先看看rsa功能的帮助:
 openssl rsa帮助
openssl rsa帮助
了解了大致参数,执行命令rsa -pubin -text -modulus -in pubkey.pem 来获取e和n的数据:
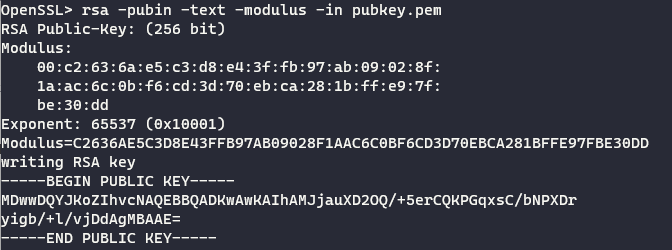
exponent就是e,modulus就是n。
这里的e是十进制的,n是十六进制的:
Exponent: 65537 (0x10001)
Modulus=C2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD
需要进行转换,使用ipython交互求出十进制数值:

现在得到:
n=87924348264132406875276140514499937145050893665602592992418171647042491658461
e=65537
下面需要求出p和q,这里需要进行大数分解,这里使用focterdb进行大数分解:

现在得到的数据有:
p=275127860351348928173285174381581152299
q=319576316814478949870590164193048041239
n=87924348264132406875276140514499937145050893665602592992418171647042491658461
e=65537
现在这些数据可以求出参数d了,这里使用rsatool求解参数d、生成私钥文件:
python ~/rsatool/rsatool.py -f PEM -o private.pem -p 275127860351348928173285174381581152299 -q 319576316814478949870590164193048041239 -e 65537
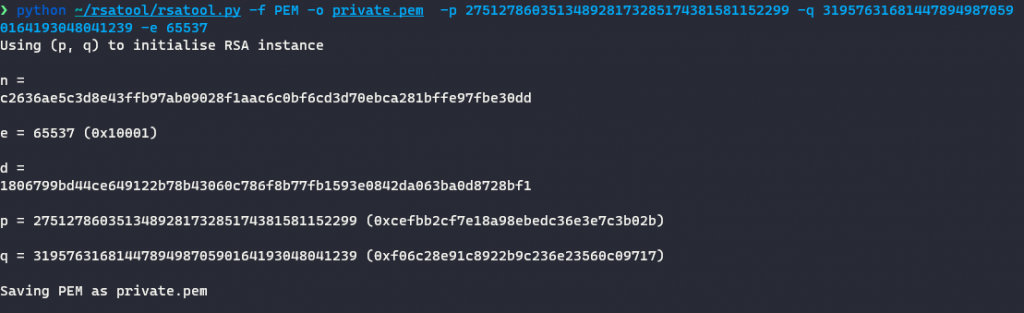
现在得到了私钥文件和公钥文件了,可以使用openssl进行解密了
opensssl解密RSA加密算法的模块是rsautl,解密之前,先看看rsautl的帮助:
了解大致参数后,执行命令开始进行求解:
rsautl -in flag.enc -inkey private.pem -out flag.txt -decrypt
然后查看生成的txt文件内容:
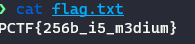
成功获取到flag数据:PCTF{256b_i5_m3dium}
题目解决,题目是比较常规的RSA题目,题目主要考察RSA知识的掌握以及RSA工具的使用。
题目难度上,题目算是简单题目。
esay_ECC
看到题目,这道题目应该是一个比较难的题目,题目考察到的是ecc加密算法,是密码学中比较难也是比较核心的考察点。ecc加密算法也是ctf密码学的难点。什么是ecc加密算法?
椭圆曲线密码学(英语:Elliptic Curve Cryptography,缩写:ECC)是一种基于椭圆曲线数学的公开密钥加密算法。椭圆曲线在密码学中的使用是在1985年由Neal Koblitz(英语:Neal Koblitz)和Victor Miller(英语:Victor Miller)分别独立提出的。
ECC的主要优势是它相比RSA加密算法使用较小的密钥长度并提供相当等级的安全性。ECC的另一个优势是可以定义群之间的双线性映射,基于Weil对或是Tate对;双线性映射已经在密码学中发现了大量的应用,例如基于身份的加密。[11]
点开题目,看看题目能给我们什么有用的信息:
 easy_ECC题目
easy_ECC题目
题目的描述提示了ecc基本原理和提交的flag格式。这道题目解决的关键应该就是ecc基本原理。
点开附件进行下载,查看附件内容:
 附件内容
附件内容
本菜鸡现在实在是看不懂ecc加密算法的基本原理,这道题目直接搬大佬的脚本求解:[12]
Gx = 6478678675
Gy = 5636379357093
a = 16546484
b = 4548674875
p = 15424654874903
k = 546768
x = Gx
y = Gy
for i in range(k-1):
if (x==Gx and y==Gy):
inv = pow(2*Gy, p-2,p)
temp = (3*Gx*Gx+a)*inv%p
else:
inv = pow((x-Gx), p-2,p)
temp = (y-Gy)*inv%p
xr = (temp*temp-Gx-x)%p
yr = (temp*(x-xr)-y)%p
#print(i,xr,yr)
x = xr
y = yr
print(x+y)
执行脚本进行求解:
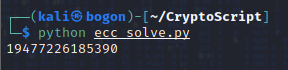
解出来的数值:19477226185390。对解出来的数值加个帽子:cyberpeace{19477226185390}
flag数据就是:cyberpeace{19477226185390}
题目解决,难度适中,主要考察ecc基本原理(本菜鸡现在看不懂,嘤嘤嘤)
参考:
- 密码学发展简史
- 凯撒密码-维基百科
- 摩尔斯电码-维基百科
- 01248云影密码-简书
- 栅栏密码-百度百科
- 培根密码-维基百科
- RSA加密算法-维基百科
- RSA加密算法-阮一峰
- 什么是.pyc文件-Python教程-PHP中文网
- 古典加密方法(三)转轮机 - block2016 - 博客园
- 椭圆曲线密码学-维基百科
- XCTF easy_ECC WP
XCTF的新手区密码学题目可能难度不是很高,但是XCTF新手区的密码学题目涉及的范围还是比较广的。从编码到密码,从古典到现代,从rsa到ecc都有涉及,密码学考察的基本知识都涉及到了。
本期wp分享到此为止,有时间再来喝杯茶呀!