BUUCTF CRYPTO (2) writeup

还是BUUCTF的题目，熟悉的感觉，再来一次！

BUUCTF首页

本次的题目大致如下：

CTF题目

题目是16道密码学题目：

传统知识+古典密码
信息化时代的步伐
RSA1
凯撒？转换？呵呵！
old-fashion
萌萌哒的八戒
权限获得第一步
世上无难事
RSA3
RSA2
异性相吸
RSA
还原大师
Unencode
robomunication
RSAROLL

题目求解：

题目都还比较简单，正常来做就好。

0x0 传统知识+古典密码

下载附件，得到题目

题目信息

应该是考察古典密码的题目，是考察六十甲子顺序纳音表的题目

这里列出六十顺序纳音表：

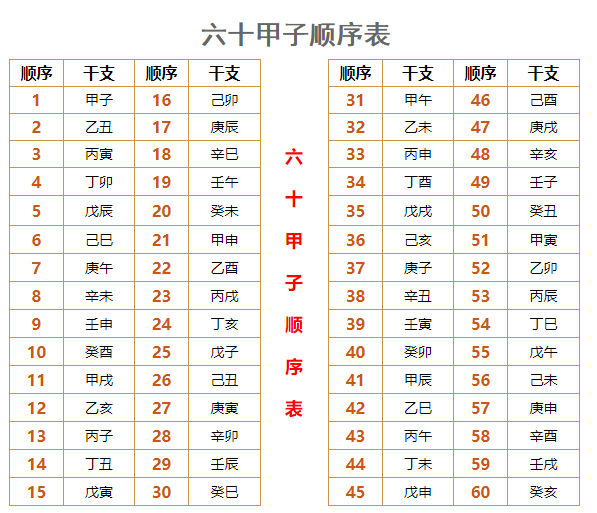
六十甲子顺序表

根据六十甲子顺序表编写python脚本：

C_sky = "甲乙丙丁戊己庚辛壬癸"
C_earth = "子丑寅卯辰巳午未申酉戌亥"
C_dict={}
for i in range(60):
    C_dict[C_sky[i%len(C_sky)]+C_earth[i%len(C_earth)]] = str(i+1)
cipher = "辛卯，癸巳，丙戌，辛未，庚辰，癸酉，己卯，癸巳"
cipher_list = cipher.split("，")
plainer = ""
for i in cipher_list:
    plainer += chr(int(C_dict[i])+60)

def decrype(cipher,key):
    cipher_len = len(cipher)
    if cipher_len%key == 0:
        key = cipher_len // key
    else:
        key = cipher_len // key + 1
    result = {x:'' for x in range(key)}
    for i in range(cipher_len):
        a = i%key;
        result.update({a:result[a]+cipher[i]})
    plainer=""
    for i in range(key):
        plainer = plainer + result[i]
    return plainer
plainer_list=[]
for n in range(2,20):
    plainer_list.append(decrype(plainer,n))

plainer_set = set(plainer_list)

def Caesar(cipher):
    dict_list = ['a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z']
    for j in range(26):
        plainer = ""
        for i in cipher:
            if i in dict_list:
                plainer += dict_list[(dict_list.index(i)-j)%26]

            else:
                plainer += i
        print(plainer.upper())

for i in plainer_set:
    Caesar(i.lower())
    print("")

说明：

脚本使用了三种加密算法，分别是传统文化加密，栅栏密码，凯撒密码

最终的输出结果是凯撒密码爆破的结果，需要进行筛选

通过简单的筛选可以得到flag为：flag{SHUANGYU}

0x1 信息化时代的步伐

审题目

应该是和中文相关的密码

看附件：

附件是一串数字，应该需要数字和中文进行联系

搜索一下：中文电码

得到了不错的搜索结果

这里涉及了一个中文电码的知识，这是一个比较偏的知识，这里可以积累一下：

中文电码，又称：中文商用电码（Chinese commercial code, CCC）、中文电报码（Chinese telegraph code, CTC）或中文电报明码（Chinese ordinary telegraph code, COTC），原本是用于电报之中传送中文信息的方法。它是第一个将汉字化作电子信号的编码表。[1]

简单来说，就是针对中文设计的一种数字编码方式。

这里直接使用在线脚本进行解码：

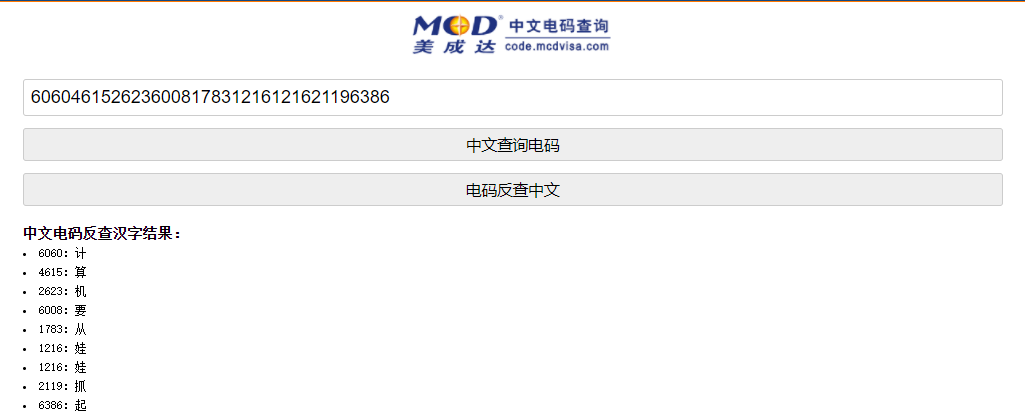
解码得出结果，即flag是flag{计算机要从娃娃抓起}

0x2 RSA1

题目考察RSA加密算法

下载附件，得到数据：

p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229 
q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469 
dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929 
dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041 
c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852

有p和q，以及dp和dq，但是没有e，n等参数

这道题目是一道典型的dp，dq泄露的RSA题目

由于涉及dp，dq参数，需要推导一下公式：

首先，最基本的RSA求值公式：

$m \equiv c^d\ mod\ n$ 和 $c \equiv m^e\ mod\ n$

然后，这里有不同于常规RSA的新参数dp和dq：

$ d_p \equiv d\ mod\ (p-1) $和 $ d_q \equiv d\ mod\ (q-1) $

下面就需要根据已知的条件进行推导：

$$ m \equiv c^d \ mod\ n \Rightarrow m = c^d + k \cdot n \Rightarrow m = c^d + k \cdot p \cdot q $$

由上面的推导可以得出：

$$ m_p \equiv c^d\ mod \ p \ m_q \equiv c^d\ mod\ q $$

进一步推导可以得出：

$$ m_p + k \cdot p = c^d$$

将上式带入到$ m_q \equiv c^d \ mod \ q $ 可得：

$$ m_q \equiv m_q + kp\ mod\ q $$

然后简单整理可得：

$$ k \equiv p^{-1} \cdot (m_q - m_p)\ mod\ q $$

故可得：

$$ m \equiv (p^{-1} \cdot (m_q-m_p)\ mod\ q ) \cdot p+ m_p \ mod \ (p \cdot q) $$

同理可得：

$$ m \equiv (p^{-1} \cdot (m_q-m_p)\ mod\ q ) \cdot q+ m_q \ mod \ (p \cdot q) $$

$$ m \equiv (q^{-1} \cdot (m_p-m_q)\ mod\ p ) \cdot p+ m_p \ mod \ (p \cdot q) $$

$$ m \equiv (q^{-1} \cdot (m_p-m_q)\ mod\ p ) \cdot q+ m_q \ mod \ (p \cdot q) $$

根据推导的公式，这里使用一个python脚本解决问题：

import gmpy2
from Crypto.Util.number import *

p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229
q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469
dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929
dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041
c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852

mp = pow(c,dp,p)
mq = pow(c,dq,q)
Ip = gmpy2.invert(p,q)
Iq = gmpy2.invert(q,p)

m1 = ((((mq-mp)*Ip)%q)*p+mp)%(p*q)
m2 = ((((mq-mp)*Ip)%q)*q+mq)%(p*q)
m3 = ((((mp-mq)*Iq)%p)*p+mp)%(p*q)
m4 = ((((mp-mq)*Iq)%p)*q+mq)%(p*q)

flag1 = long_to_bytes(m1)
flag2 = long_to_bytes(m2)
flag3 = long_to_bytes(m3)
flag4 = long_to_bytes(m4)

print "flag:{}".format(flag1)
print "flag:{}".format(flag2)
print "flag:{}".format(flag3)
print "flag:{}".format(flag4)

脚本运行即得到flag，即noxCTF{W31c0m3_70_Ch1n470wn}

根据题目要求，故flag： flag{W31c0m3_70_Ch1n470wn}

0x3 凯撒？转换？呵呵！

题目应该是考察变种凯撒加密的

MTHJ{CUBCGXGUGXWREXIPOYAOEYFIGXWRXCHTKHFCOHCFDUCGTXZOHIXOEOWMEHZO}
注意：得到的 flag 请包上 flag{} 提交, flag{小写字母}

这里使用一个在线工具进行求解

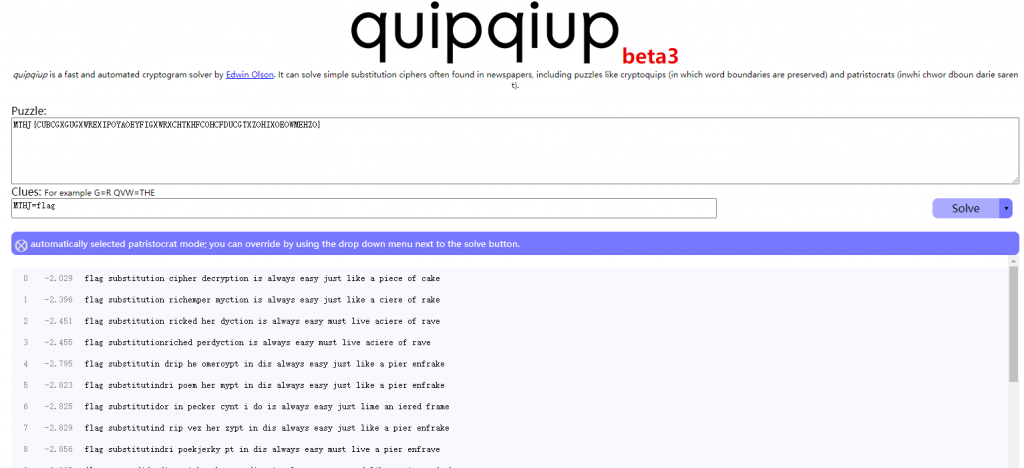
通过在线工具就得到flag，即flag{substitutioncipherdecryptionisalwayseasyjustlikeapieceofcake}

“忘了是否要进行大小写转换，题目的思路大致就是这样了”

0x4 old-fashion

题目描述没什么好说的，直接下载附件，查看附件

Os drnuzearyuwn, y jtkjzoztzoes douwlr oj y ilzwex eq lsdexosa kn pwodw tsozj eq ufyoszlbz yrl rlufydlx pozw douwlrzlbz, ydderxosa ze y rlatfyr jnjzli; mjy gfbmw vla xy wbfnsy symmyew (mjy vrwm qrvvrf), hlbew rd symmyew, mebhsymw rd symmyew, vbomgeyw rd mjy lxrzy, lfk wr dremj. Mjy eyqybzye kyqbhjyew mjy myom xa hyedrevbfn lf bfzyewy wgxwmbmgmbrf. Wr mjy dsln bw f1_2jyf-k3_jg1-vb-vl_l

一段文字，直接丢在线工具里面进行词频分析吧：

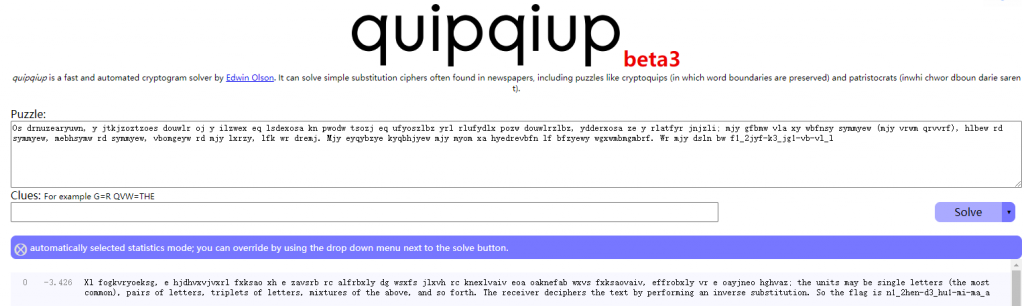
得到词频分析结果：

Xl fogkvryoeksg, e hjdhvxvjvxrl fxksao xh e zavsrb rc alfrbxly dg wsxfs jlxvh rc knexlvaiv eoa oaknefab wxvs fxksaovaiv, effrobxly vr e oayjneo hghvaz; the units may be single letters (the most common), pairs of letters, triplets of letters, mixtures of the above, and so forth. The receiver deciphers the text by performing an inverse substitution. So the flag is n1_2hen-d3_hu1-mi-ma_a

故得flag：flag{n1_2hen-d3_hu1-mi-ma_a}

0x5 萌萌哒的八戒

萌萌哒的八戒，应该是猪圈密码

什么是猪圈密码？

猪圈密码（英语：pigpen cipher)，亦称共济会密码（masonic cipher）或共济会员密码（Freemason’s cipher），是一种以格子为基础的简单替代式密码。即使使用符号，也不会影响密码分析，亦可用在其它替代式的方法。右边的例子，是把字母填进格子的模样。

早在1700年代，共济会常常使用这种密码保护一些私密纪录或用来通讯，所以又称共济会密码。[2]

萌萌哒的八戒原来曾经是猪村的村长，从远古时期，猪村就有一种神秘的代码。请从附件中找出代码，看看萌萌哒的猪八戒到底想说啥 注意：得到的 flag 请包上 flag{} 提交

题目描述正好和猜想对应，下载附件，查看附件

得到一张图片:

下面那一串应该就是猪圈密码，进行解密：

这里使用在线工具进行解密：

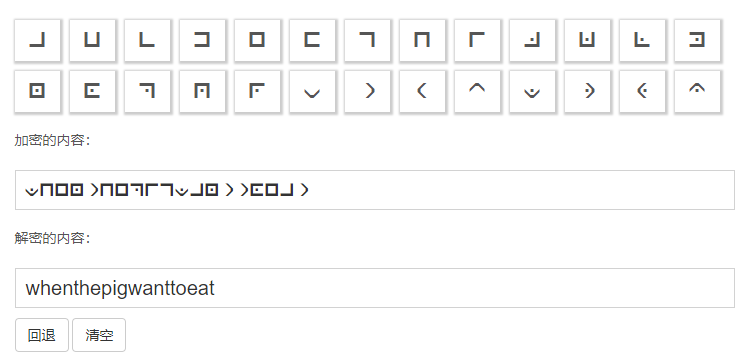
得到flag，即flag{whenthepigwanttoeat}

0x6 权限获得第一步

这题应该是使用哈希密码破解的方法进行解密

下载附件，查看附件内容：

Administrator:500:806EDC27AA52E314AAD3B435B51404EE:F4AD50F57683D4260DFD48AA351A17A8:::

密文明显是windows系统的hash加密，第一段的哈希加密应该是Administrator的用户名，第二段的哈希加密应该是windows系统的密码

直接对第二段哈希值进行哈希破解：

这里使用在线工具进行破解：

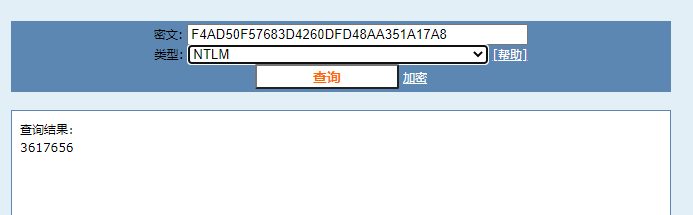
故flag即为flag{3617656}

0x7 世上无难事

打开题目：

以下是某国现任总统外发的一段指令，经过一种奇异的加密方式，毫无规律，看来只能分析了。请将这段语句还原成通顺语句，并从中找到key作为答案提交，答案是32位，包含小写字母。 注意：得到的 flag 请包上 flag{} 提交

下载附件，查看附件：

VIZZB IFIUOJBWO NVXAP OBC XZZ UKHVN IFIUOJBWO HB XVIXW XAW VXFI X QIXN VBD KQ IFIUOJBWO WBKAH NBWXO VBD XJBCN NKG QLKEIU DI XUI VIUI DKNV QNCWIANQ XN DXPIMKIZW VKHV QEVBBZ KA XUZKAHNBA FKUHKAKX XAW DI VXFI HBN QNCWIANQ NCAKAH KA MUBG XZZ XEUBQQ XGIUKEX MUBG PKAWIUHXUNIA NVUBCHV 12NV HUXWI XAW DI XUI SCQN QB HZXW NVXN XZZ EBCZW SBKA CQ NBWXO XAW DI DXAN NB NVXAP DXPIMKIZW MBU JIKAH QCEV XA BCNQNXAWKAH VBQN HKFI OBCUQIZFIQ X JKH UBCAW BM XLLZXCQI XAW NVI PIO KQ 640I11012805M211J0XJ24MM02X1IW09

得到一段文字，直接丢到在线工具得：

HELLO EVERYBODY THANK YOU ALL RIGHT EVERYBODY GO AHEAD AND HAVE A SEAT HOW IS EVERYBODY DOING TODAY HOW ABOUT TIM SPICER WE ARE HERE WITH STUDENTS AT WAKEFIELD HIGH SCHOOL IN ARLINGTON VIRGINIA AND WE HAVE GOT STUDENTS TUNING IN FROM ALL ACROSS AMERICA FROM KINDERGARTEN THROUGH 12TH GRADE AND WE ARE JUST SO GLAD THAT ALL COULD JOIN US TODAY AND WE WANT TO THANK WAKEFIELD FOR BEING SUCH AN OUTSTANDING HOST GIVE YOURSELVES A BIG ROUND OF APPLAUSE AND THE KEY IS 640E11012805F211B0AB24FF02A1ED09

得到flag，即flag为flag{640e11012805f211b0ab24ff02a1ed09}

0x8 RSA3

RSA题目，直接下载附件，查看附件：

c1=22322035275663237041646893770451933509324701913484303338076210603542612758956262869640822486470121149424485571361007421293675516338822195280313794991136048140918842471219840263536338886250492682739436410013436651161720725855484866690084788721349555662019879081501113222996123305533009325964377798892703161521852805956811219563883312896330156298621674684353919547558127920925706842808914762199011054955816534977675267395009575347820387073483928425066536361482774892370969520740304287456555508933372782327506569010772537497541764311429052216291198932092617792645253901478910801592878203564861118912045464959832566051361
n=22708078815885011462462049064339185898712439277226831073457888403129378547350292420267016551819052430779004755846649044001024141485283286483130702616057274698473611149508798869706347501931583117632710700787228016480127677393649929530416598686027354216422565934459015161927613607902831542857977859612596282353679327773303727004407262197231586324599181983572622404590354084541788062262164510140605868122410388090174420147752408554129789760902300898046273909007852818474030770699647647363015102118956737673941354217692696044969695308506436573142565573487583507037356944848039864382339216266670673567488871508925311154801
e1=11187289
c2=18702010045187015556548691642394982835669262147230212731309938675226458555210425972429418449273410535387985931036711854265623905066805665751803269106880746769003478900791099590239513925449748814075904017471585572848473556490565450062664706449128415834787961947266259789785962922238701134079720414228414066193071495304612341052987455615930023536823801499269773357186087452747500840640419365011554421183037505653461286732740983702740822671148045619497667184586123657285604061875653909567822328914065337797733444640351518775487649819978262363617265797982843179630888729407238496650987720428708217115257989007867331698397
e2=9647291

看到c1，c2，e1，e2应该是RSA共模攻击

RSA共模攻击需要使用到扩展欧几里得定理：

扩展欧几里得算法是欧几里得算法（又叫辗转相除法）的扩展。除了计算a、b两个整数的最大公约数，此算法还能找到整数x、y（其中一个很可能是负数）。通常谈到最大公因子时, 我们都会提到一个非常基本的事实: 给予二整数 a 与 b, 必存在有整数 x 与 y 使得$ ax + by = gcd(a,b) $。有两个数a,b，对它们进行辗转相除法，可得它们的最大公约数——这是众所周知的。然后，收集辗转相除法中产生的式子，倒回去，可以得到$ ax+by=gcd(a,b) $的整数解。[3]

根据维基百科，可以找到扩展欧几里得定理的python算法 [4] :

def ext_euclid(a, b):
    old_s,s=1,0
    old_t,t=0,1
    old_r,r=a,b
    if b == 0:
        return 1, 0, a
    else:
        while(r!=0):
            q=old_r//r
            old_r,r=r,old_r-q*r
            old_s,s=s,old_s-q*s
            old_t,t=t,old_t-q*t
    return old_s, old_t, old_r

这里根据题目要求，使用一个python脚本解决题目：

from gmpy2 import invert
from Crypto.Util.number import *

def gongmo(n, c1, c2, e1, e2):
    def egcd(a, b):
        if b == 0:
            return a, 0
        else:
            x, y = egcd(b, a % b)
            return y, x - (a // b) * y
    s = egcd(e1, e2)
    s1 = s[0]
    s2 = s[1]

    if s1 < 0:
        s1 = - s1
        c1 = invert(c1, n)
    elif s2 < 0:
        s2 = - s2
        c2 = invert(c2, n)
    m = pow(c1, s1, n) * pow(c2, s2, n) % n
    return m

c1=22322035275663237041646893770451933509324701913484303338076210603542612758956262869640822486470121149424485571361007421293675516338822195280313794991136048140918842471219840263536338886250492682739436410013436651161720725855484866690084788721349555662019879081501113222996123305533009325964377798892703161521852805956811219563883312896330156298621674684353919547558127920925706842808914762199011054955816534977675267395009575347820387073483928425066536361482774892370969520740304287456555508933372782327506569010772537497541764311429052216291198932092617792645253901478910801592878203564861118912045464959832566051361
n=22708078815885011462462049064339185898712439277226831073457888403129378547350292420267016551819052430779004755846649044001024141485283286483130702616057274698473611149508798869706347501931583117632710700787228016480127677393649929530416598686027354216422565934459015161927613607902831542857977859612596282353679327773303727004407262197231586324599181983572622404590354084541788062262164510140605868122410388090174420147752408554129789760902300898046273909007852818474030770699647647363015102118956737673941354217692696044969695308506436573142565573487583507037356944848039864382339216266670673567488871508925311154801
e1=11187289
c2=18702010045187015556548691642394982835669262147230212731309938675226458555210425972429418449273410535387985931036711854265623905066805665751803269106880746769003478900791099590239513925449748814075904017471585572848473556490565450062664706449128415834787961947266259789785962922238701134079720414228414066193071495304612341052987455615930023536823801499269773357186087452747500840640419365011554421183037505653461286732740983702740822671148045619497667184586123657285604061875653909567822328914065337797733444640351518775487649819978262363617265797982843179630888729407238496650987720428708217115257989007867331698397
e2=9647291

result = gongmo(n, c1, c2, e1, e2)

print long_to_bytes(result)

根据脚本可以直接求出flag：flag{49d91077a1abcb14f1a9d546c80be9ef}

0x9 RSA2

直接下载附件，打开附件：

e = 65537
n = 248254007851526241177721526698901802985832766176221609612258877371620580060433101538328030305219918697643619814200930679612109885533801335348445023751670478437073055544724280684733298051599167660303645183146161497485358633681492129668802402065797789905550489547645118787266601929429724133167768465309665906113
dp = 905074498052346904643025132879518330691925174573054004621877253318682675055421970943552016695528560364834446303196939207056642927148093290374440210503657

c = 140423670976252696807533673586209400575664282100684119784203527124521188996403826597436883766041879067494280957410201958935737360380801845453829293997433414188838725751796261702622028587211560353362847191060306578510511380965162133472698713063592621028959167072781482562673683090590521214218071160287665180751

题目考察的应该就是典型的dp泄露问题，这里就进行简单的公式推导： $$ n = p \cdot q $$

$$ \varphi(n) = (p-1) \cdot (q-1) $$

$$ d_p \equiv d\ mod\ (p-1) $$

$$ d \equiv e^{-1}\ mod\ \varphi(n) $$

根据已知信息进行推导：

$$ d = e^{-1} + k(p-1)(q-1) \Rightarrow dp \equiv e^{-1} mod\ (p-1)\ $$

同理，也可以推导出：

$$ d = e^{-1} + k(p-1)(q-1) \Rightarrow dp \equiv e^{-1} mod\ (q-1)\ $$

易得：

$$ dp \cdot e -1 = k \cdot (q-1) $$

爆破出k即可求得的q值，进一步即可求得结果，这里使用一个python脚本求解：

from Crypto.Util.number import *
import gmpy2

e = 65537
n = 248254007851526241177721526698901802985832766176221609612258877371620580060433101538328030305219918697643619814200930679612109885533801335348445023751670478437073055544724280684733298051599167660303645183146161497485358633681492129668802402065797789905550489547645118787266601929429724133167768465309665906113
dp = 905074498052346904643025132879518330691925174573054004621877253318682675055421970943552016695528560364834446303196939207056642927148093290374440210503657

c = 140423670976252696807533673586209400575664282100684119784203527124521188996403826597436883766041879067494280957410201958935737360380801845453829293997433414188838725751796261702622028587211560353362847191060306578510511380965162133472698713063592621028959167072781482562673683090590521214218071160287665180751

temp = dp *e
for i in range(1,e):
    if (temp-1)%i == 0:
        x = (temp-1)//i + 1
        y = n%x
        if y == 0:
            p=x
            break
q = n // p

# print p
# print q

phi = (q-1)*(p-1)
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
flag = long_to_bytes(m)
print flag

运行脚本即可求出flag：flag{wow_leaking_dp_breaks_rsa?_98924743502}

0xA 异性相吸

看题目，应该是考察异或操作的题目

下载附件，查看附件

附件内容

两个文件，应该是使用异或处理最终得到结果，这里使用一个python脚本进行文件的二进制数据读取，然后进行异或操作求解出flag：

# env = python3
from Crypto.Util.number import *
import struct

# 读取key.txt文件
key = open("key.txt",mode="rb")
k = key.read()
key.close()

# 读取密文.txt文件
cipher = open("密文.txt",mode="rb")
c = cipher.read()
cipher.close()

# 文件二进制数据进行异或处理
m=int.from_bytes(c,byteorder="big",signed=True)^int.from_bytes(k,byteorder="big",signed=True)

# 求解flag
flag = long_to_bytes(m).decode()

print(flag)

运行脚本得到flag：flag{ea1bc0988992276b7f95b54a7435e89e}

0xB RSA

RSA题目，直接下载附件，查看附件

附件内容

常规的RSA题目，使用openssl工具进行公钥文件的读取和私钥文件的解密

首先使用openssl对公钥文件进行解析：

> openssl rsa -pubin -in pub.key -modulus -text
RSA Public-Key: (256 bit)
Modulus:
    00:c0:33:2c:5c:64:ae:47:18:2f:6c:1c:87:6d:42:
    33:69:10:54:5a:58:f7:ee:fe:fc:0b:ca:af:5a:f3:
    41:cc:dd
Exponent: 65537 (0x10001)
Modulus=C0332C5C64AE47182F6C1C876D42336910545A58F7EEFEFC0BCAAF5AF341CCDD
writing RSA key
-----BEGIN PUBLIC KEY-----
MDwwDQYJKoZIhvcNAQEBBQADKwAwKAIhAMAzLFxkrkcYL2wch21CM2kQVFpY9+7+
/AvKr1rzQczdAgMBAAE=
-----END PUBLIC KEY-----

获得到了n和e

n = 0xC0332C5C64AE47182F6C1C876D42336910545A58F7EEFEFC0BCAAF5AF341CCDD
e = 65537

使用factordb进行大数分解

得到p和q：

p=285960468890451637935629440372639283459
q=304008741604601924494328155975272418463

根据已知的信息，编写python脚本，来获取flag：

# 
import rsa
import libnum

e = 65537
n = 86934482296048119190666062003494800588905656017203025617216654058378322103517
p = 285960468890451637935629440372639283459
q = 304008741604601924494328155975272418463
d = libnum.invmod(e,(p-1)*(q-1))

key = rsa.PrivateKey(n,e,d,p,q)

with open("flag.enc","rb") as f:
    f = f.read()
    flag = rsa.decrypt(f,key).decode()
    print(flag)

执行脚本，获取到flag：flag{decrypt_256}

0xC 还原大师

打开题目描述：

我们得到了一串神秘字符串：TASC?O3RJMV?WDJKX?ZM,问号部分是未知大写字母，为了确定这个神秘字符串，我们通过了其他途径获得了这个字串的32位MD5码。但是我们获得它的32位MD5码也是残缺不全，E903???4DAB????08?????51?80??8A?,请猜出神秘字符串的原本模样，并且提交这个字串的32位MD5码作为答案。 注意：得到的 flag 请包上 flag{} 提交

题目应该是考察md5加密的暴力破解来还原md5的数值：

根据题目要求编写python脚本进行还原：

import hashlib
cipher_dict=[]
for i in range(65,91):
    cipher_dict.append(chr(i))

def md5_encrypt(m):
    return hashlib.md5(m).hexdigest()

cipher="TASC?O3RJMV?WDJKX?ZM"
cipher_list=[]
while "?" in cipher:
    index = 0
    cipher_list.append(cipher[:cipher.index("?")])
    cipher = cipher[cipher.index("?")+1:]

cipher_list.append(cipher)

for i in cipher_dict:
    for j in cipher_dict:
        for k in cipher_dict:
            md5_str =md5_encrypt(cipher_list[0]+i+cipher_list[1]+j+cipher_list[2]+k+cipher_list[3]).upper()
            if md5_str[:4] == "E903":
                print "flag{"+md5_str+"}"
                print "flag{"+md5_str.lower()+"}"
                break

运行脚本就可以获得flag，结果有大写和小写，忘记了具体是要求提交小写flag和大写flag。

运行结果：

flag{E9032994DABAC08080091151380478A2}
flag{e9032994dabac08080091151380478a2}

0xD Unencode

看题目应该是考察UUencode编码的题目

下载附件，查看附件：

89FQA9WMD<V1A<V1S83DY.#<W3$Q,2TM]

丢在线工具里面进行解码：

解码即可获得flag：flag{dsdasdsa99877LLLKK}

0xE robomunication

直接下载附件，查看附件：

附件内容

发现是一个音频文件，听出来是如下内容：

bbbb b bpbb bpbb ppp bpp bbbb bp p bb bbb p bbbb b pbp b pbpp bb p bb bbb pbbb ppp ppp bppb pbbb b b bppb

发现是一个摩尔斯电码加密，破译得：

HELLOWHATISTHEKEYITISBOOPBEEP

对单词进行分割可得：

HELLO WHAT IS THE KEY IT IS BOOPBEEP

故flag是flag:flag{BOOPBEEP}

0xF RSAROLL

RSA题目，直接下载附件，查看附件

题目.txt

RSA roll！roll！roll！
Only number and a-z
（don't use editor
which MS provide）

data.txt

{920139713,19}

704796792
752211152
274704164
18414022
368270835
483295235
263072905
459788476
483295235
459788476
663551792
475206804
459788476
428313374
475206804
459788476
425392137
704796792
458265677
341524652
483295235
534149509
425392137
428313374
425392137
341524652
458265677
263072905
483295235
828509797
341524652
425392137
475206804
428313374
483295235
475206804
459788476
306220148

题目考查RSA低加密指数攻击，但是这道题目，可以试试分解一下n然后进行一下拼接

首先可以先去在线网站进行大数分解：

得到p和q的数值

p = 18443
q = 49891

然后使用一个python脚本解决问题：

import libnum
from Crypto.Util.number import *

pub_str = ""
cipher_list=[]
with open("data.txt") as f:
    lines = f.readlines()
    for line in lines:
        line = line.strip("\n")
        if "{" in line:
            pub_str = line[1:-1]
        elif line != "":
            cipher_list.append(line)

pub_list= pub_str.split(",")
n = int(pub_list[0])
e = int(pub_list[1])
p = 18443
q = 49891
phi = (p-1)*(q-1)
d = libnum.invmod(e,phi)

flag = ""
for i in cipher_list:
    m = pow(int(i),d,n)
    plainer = long_to_bytes(m)
    flag += plainer

print flag

运行脚本获得flag，即flag{13212je2ue28fy71w8u87y31r78eu1e2}

参考：

[标准中文电码(Chinese Commercial Code)简介、用途及查询](https://www.chasedream.com/show.aspx?id=4487&cid=30#:~:text=中文电码，又称：中文商用电码（Chinese commercial code%2C CCC）、中文电报码（Chinese telegraph,code%2C CTC）或中文电报明码（Chinese ordinary telegraph code%2C COTC），原本是用于电报之中传送中文信息的方法。)
猪圈密码-维基百科
[扩展欧几里得算法-百度百科](https://baike.baidu.com/item/扩展欧几里得算法/2029414?fromtitle=扩展欧几里德算法&fromid=1053275#:~:text=扩展欧几里得算法（英语：Extended Euclidean algorithm）是欧几里得算法（又叫辗转相除法）的扩展。已知整数a、b，扩展欧几里得算法可以在求得a、b的最大公约数,by %3D gcd (a%2Cb) 。有两个数a%2Cb，对它们进行辗转相除法，可得它们的最大公约数——这是众所周知的。然后，收集辗转相除法中产生的式子，倒回去，可以得到ax%2Bby%3Dgcd (a%2Cb)的整数解。)
[扩展欧几里得算法-维基百科](https://baike.baidu.com/item/扩展欧几里得算法/2029414?fromtitle=扩展欧几里德算法&fromid=1053275#:~:text=扩展欧几里得算法（英语：Extended Euclidean algorithm）是欧几里得算法（又叫辗转相除法）的扩展。已知整数a、b，扩展欧几里得算法可以在求得a、b的最大公约数,by %3D gcd (a%2Cb) 。有两个数a%2Cb，对它们进行辗转相除法，可得它们的最大公约数——这是众所周知的。然后，收集辗转相除法中产生的式子，倒回去，可以得到ax%2Bby%3Dgcd (a%2Cb)的整数解。)

本期wp分享到此为止，有时间再来喝杯茶呀！