BUUCTF CRYPTO (1) writeup

日常刷题喝茶的平时生活，整理一下题目的思路，捋一捋密码学。

BUUCTF是国内另一个比较不错的CTF的刷题平台，是由北京联合大学创建并维护的CTF大型同性交流沟通的平台，页面制作还是蛮美观滴！

BUUCTF页面

BUUCTF的整体难度是由简单变难的一个过程，前面的题目通常都是比较简单的题目，来看看这次日常的题目：

题目

这次是16道题目：

MD5
Url编码
一眼就解密
看我回旋踢
摩丝
password
变异凯撒
Quoted-printable
Rabbit
篱笆墙的影子
RSA
丢失的MD5
Alice与Bob
rsarsa
大帝的密码武器
Windows系统密码

MD5

看题目应该是考察MD5加密的暴力破解

什么是MD5加密？

MD5消息摘要算法（英语：MD5 Message-Digest Algorithm），一种被广泛使用的密码散列函数，可以产生出一个128位（16字节）的散列值（hash value），用于确保信息传输完整一致。MD5由美国密码学家罗纳德·李维斯特（Ronald Linn Rivest）设计，于1992年公开，用以取代MD4算法。这套算法的程序在 RFC 1321 中被加以规范。

将数据（如一段文字）运算变为另一固定长度值，是散列算法的基础原理。

1996年后被证实存在弱点，可以被加以破解，对于需要高度安全性的资料，专家一般建议改用其他算法，如SHA-2。2004年，证实MD5算法无法防止碰撞攻击（英语：Collision_attack），因此不适用于安全性认证，如SSL公开密钥认证或是数字签名等用途。[1]

看看题目描述：

题目描述

下载附件，查看附件内容：

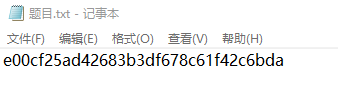
附件内容

附件中给出一段加密数据：e00cf25ad42683b3df678c61f42c6bda

根据题目，应该是MD5加密，去解密网站

进行解密。

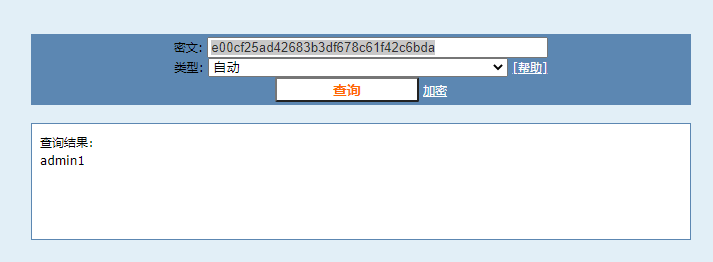cmd5

题目描述中，要求以flag{}形式进行提交，故flag就是flag{admin1}

这道题目考察md5加密的相关知识，签到题。

Url编码

看题目应该是考察Url编码的解码

什么是Url编码？

百分号编码（英语：Percent-encoding），又称：URL编码（URL encoding）是特定上下文的统一资源定位符（URL）的编码机制，实际上也适用于统一资源标志符（URI）的编码。也用于为 application/x-www-form-urlencoded MIME准备数据，因为它用于通过HTTP的请求操作（request）提交HTML表单数据。[2]

看看题目描述：

题目描述

下载附件，查看附件内容：

附件内容

一段编码的字段：%66%6c%61%67%7b%61%6e%64%20%31%3d%31%7d

使用url解码工具解码，也可以使用python进行解码。我个人习惯使用python脚本进行url编码解码：

import urllib.parse

cipher = '%66%6c%61%67%7b%61%6e%64%20%31%3d%31%7d'
print(urllib.parse.unquote(cipher))

运行脚本就可以出结果：

解码后也就是flag数据：flag{and 1=1}

故本题的flag是flag{and 1=1}

题目主要考察URL编码，签到题。

一眼就解密

题目给不了太多提示

直接点开题目描述看内容：

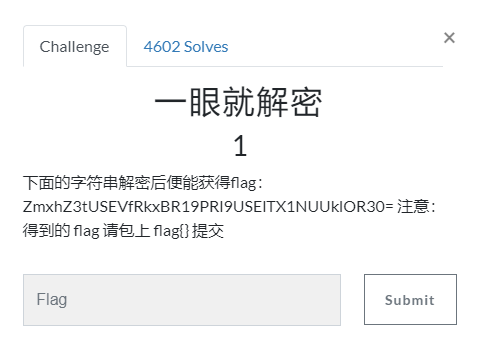
题目描述

看题目描述中的字符串，字符串的样子像是base64编码：ZmxhZ3tUSEVfRkxBR19PRl9USElTX1NUUklOR30=

这里一个脚本进行求解：

import base64

cipher = "ZmxhZ3tUSEVfRkxBR19PRl9USElTX1NUUklOR30="
plainer = ""

plainer = base64.b64decode(cipher)
print plainer

运行程序求解得到：flag{THE_FLAG_OF_THIS_STRING}

故本题的flag是flag{THE_FLAG_OF_THIS_STRING}

题目考察base64编码，签到题。

看我回旋踢

看题目，暂时想不出什么密码相关联的内容。

点开题目描述：

题目描述

只提示了题目提交的flag数据的格式信息

下载附件，查看附件内容：

附件内容

看附件给出的字符形式像是替换密码加密的数据，最容易联想到的替换密码就是凯撒密码，尝试使用凯撒密码进行解密：（这里一个脚本求解凯撒密码）

dict_list = []
for i in range(26):
    dict_list.append(chr(ord('a')+i))

cipher = "synt{5pq1004q-86n5-46q8-o720-oro5on0417r1}"

for n in range(26):
    plainer = ""
    for i in cipher:
        if i in dict_list:
            plainer += dict_list[(dict_list.index(i)-n)%26]
        else:
            plainer += i

    print plainer

凯撒密码的算法思路，在上一篇XCTF CRYPTO的WP中有提到，具体内容可以访问上一篇：

XCTF-CRYPTO-新手区 writeup

运行脚本程序，得到一堆凯撒解密的结果：

synt{5pq1004q-86n5-46q8-o720-oro5on0417r1}
rxms{5op1004p-86m5-46p8-n720-nqn5nm0417q1}
qwlr{5no1004o-86l5-46o8-m720-mpm5ml0417p1}
pvkq{5mn1004n-86k5-46n8-l720-lol5lk0417o1}
oujp{5lm1004m-86j5-46m8-k720-knk5kj0417n1}
ntio{5kl1004l-86i5-46l8-j720-jmj5ji0417m1}
mshn{5jk1004k-86h5-46k8-i720-ili5ih0417l1}
lrgm{5ij1004j-86g5-46j8-h720-hkh5hg0417k1}
kqfl{5hi1004i-86f5-46i8-g720-gjg5gf0417j1}
jpek{5gh1004h-86e5-46h8-f720-fif5fe0417i1}
iodj{5fg1004g-86d5-46g8-e720-ehe5ed0417h1}
hnci{5ef1004f-86c5-46f8-d720-dgd5dc0417g1}
gmbh{5de1004e-86b5-46e8-c720-cfc5cb0417f1}
flag{5cd1004d-86a5-46d8-b720-beb5ba0417e1}
ekzf{5bc1004c-86z5-46c8-a720-ada5az0417d1}
djye{5ab1004b-86y5-46b8-z720-zcz5zy0417c1}
cixd{5za1004a-86x5-46a8-y720-yby5yx0417b1}
bhwc{5yz1004z-86w5-46z8-x720-xax5xw0417a1}
agvb{5xy1004y-86v5-46y8-w720-wzw5wv0417z1}
zfua{5wx1004x-86u5-46x8-v720-vyv5vu0417y1}
yetz{5vw1004w-86t5-46w8-u720-uxu5ut0417x1}
xdsy{5uv1004v-86s5-46v8-t720-twt5ts0417w1}
wcrx{5tu1004u-86r5-46u8-s720-svs5sr0417v1}
vbqw{5st1004t-86q5-46t8-r720-rur5rq0417u1}
uapv{5rs1004s-86p5-46s8-q720-qtq5qp0417t1}
tzou{5qr1004r-86o5-46r8-p720-psp5po0417s1}

在解密的字符列表中，找到符合flag格式的字符段：

flag{5cd1004d-86a5-46d8-b720-beb5ba0417e1}

故本题的flag是：flag{5cd1004d-86a5-46d8-b720-beb5ba0417e1}

题目主要考察凯撒密码，签到题。

摩丝

看题目，可以联想到Morse电码，这题目应该是摩尔斯密码的解密题目

点开题目描述：

题目描述

题目描述只说了flag{}的格式，下载附件并查看：

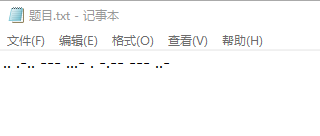
附件内容

果然是摩尔斯密码，这里一个脚本解决：

dict_list = {
        '.-':'a',
        '-...':'b',
        '-.-.':'c',
        '-..':'d',
        '.':'e',
        '..-.':'f',
        '--.':'g',
        '....':'h',
        '..':'i',
        '.---':'j',
        '-.-':'k',
        '.-..':'l',
        '--':'m',
        '-.':'n',
        '---':'o',
        '.--.':'p',
        '--.-':'q',
        '.-.':'r',
        '...':'s',
        '-':'t',
        '..-':'u',
        '...-':'v',
        '.--':'w',
        '-..-':'x',
        '-.--':'y',
        '--..':'z',
        '-----':'0',
        '.----':'1',
        '..---':'2',
        '...--':'3',
        '....-':'4',
        '.....':'5',
        '-....':'6',
        '--...':'7',
        '---..':'8',
        '----.':'9',
        '..--.-':'_'
        }
cipher = ".. .-.. --- ...- . -.-- --- ..-"
plainer = ""

cipher_arr = cipher.split(" ")

for i in cipher_arr:
    plainer += dict_list[i]

print plainer.upper()
print plainer.lower()

摩尔斯电码的详细介绍，在上一篇XCTF CRYPTO的WP中有提到，具体内容可以访问上一篇：

XCTF-CRYPTO-新手区 writeup

执行一下代码，得到两个数据：

ILOVEYOU
iloveyou

两个数据都可能是flag数据，我记得这道题目的flag数据好像是用大写的，即：flag{ILOVEYOU}，也有可能错。

题目主要考察摩尔斯电码相关知识，签到题。

password

看题目应该是与密码有关系的题目

点开题目描述：

题目描述

只有flag数据提交格式的相关信息，下载附件并打开：

附件内容

看到附件内容里面的信息，可以大致判断这道题目应该是社会工程学题目。

什么是社会工程学：

在计算机科学，社会工程学指的是通过与他人的合法交流，来使其心理受到影响，做出某些动作或者是透露一些机密信息的方式。这通常被认为是欺诈他人以收集信息、行骗和入侵计算机系统的行为。在英美普通法系，这一行为一般是被认作侵犯隐私权的。

历史上，社会工程学是隶属于社会学，不过其影响他人心理的效果引起了计算机安全专家的注意。3

简单来说，社会工程学就是利用人性的弱点来进行分析，得到关键性的信息的方式。社会工程学也就是互联网安全体系中存在的威胁性漏洞。

根据题目的信息，可以猜测flag数据可能是flag{zs19900315}或flag{19900315zs}

经过测试发现，flag数据是flag{zs19900315}

题目主要考察社会工程学的知识，签到题。

变异凯撒

看题目应该是凯撒密码考察

点开题目描述：

题目描述

题目描述一如既往的朴素，只告诉了提交的格式

下载附件，并查看附件内容：

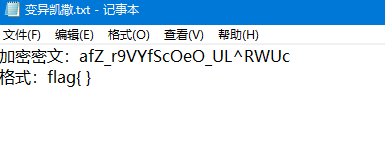
附件内容

密文中有很多编码的字符，字典集可能不是26字母表，可能是ascii编码表

分析一下附件的加密逻辑：（这里我写了一个小脚本）

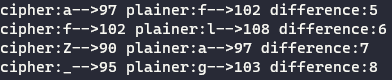分析

分析发现移位是ascii码的移位方式，而且移位的数据是一个递增的数列，5作为初始数列，以1为差值的等差数列形式。明文的数值比密文的数值大一些。分析完毕。

这里还是一个脚本解决问题：

cipher = "afZ_r9VYfScOeO_UL^RWUc"
plainer = ""

num = 5
for i in cipher:
    plainer +=chr(ord(i)+num)
    num += 1

print plainer

执行脚本，得到flag数据：flag{Caesar_variation}

故flag数据是flag{Caesar_variation}

题目主要考察凯撒密码的原理，简单题。

Quoted-printable

题目暂时看不出什么样的信息，题目翻译下来就是字符集

点开题目描述：

题目描述

题目描述还是一如既往的buu的风格，没有什么提示性的描述

直接下载附件，并查看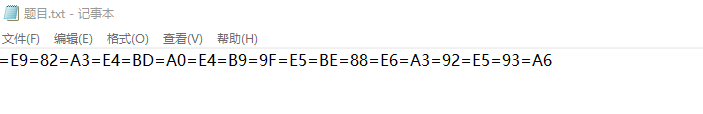附件内容：

附件内容

看到内容，感觉是熟悉的味道：E9=82=A3=E4=BD=A0=E4=B9=9F=E5=BE=88=E6=A3=92=E5=93=A6

这里写个小脚本试试16进制解码：

cipher = "E9=82=A3=E4=BD=A0=E4=B9=9F=E5=BE=88=E6=A3=92=E5=93=A6"
cipher_arr = cipher.split('=')
plainer = ''.join(cipher_arr).decode('hex')
print plainer

执行编写的脚本，得到数据：那你也很棒哦

这个数据应该就是flag数据了，对数据进行一些修饰得到flag：flag{那你也很棒哦}

故flag是flag{那你也很棒哦}

本题主要考察hex编码，签到题。

Rabbit

看到题目名字还是有些懵懵的，搜索一些发现题目应该是在说Rabbit流密码。

什么是流密码？什么是Rabbit密码？

在密码学中，流密码（英语：Stream cipher），又译为流加密、资料流加密，是一种对称加密算法，加密和解密双方使用相同伪随机加密数据流（pseudo-random stream）作为密钥，明文数据每次与密钥数据流顺次对应加密，得到密文数据流。实践中数据通常是一个位（bit）并用异或（xor）操作加密。

该算法解决了对称加密完善保密性（perfect secrecy）的实际操作困难。“完善保密性”由克劳德·香农于1949年提出。由于完善保密性要求密钥长度不短于明文长度，故而实际操作存在困难，改由较短数据流通过特定算法得到密钥流。[4]

流密码就是基于随机数的对称加密算法，Rabbit密码是流密码的一种：

Rabbit流密码（Rabbit Stream Cipher）简介

Rabbit流密码是由Cryptico公司（http://www.cryptico.com）设计的，密钥长度128位，

最大加密消息长度为2 Bytes，即16 TB，若消息超过该长度，则需要更换密钥对剩下的消息进行处理。它是目前安全性较高，加/解密速度比较高效的流密码之一，在各种处理器平台上都有不凡的表现。[5]

Cryptico公司好像是已经搜索不到了，而且那个网站的域名也在进行拍卖，以目前的情况，我还找不到有关Rabbit密码的相关算法信息。但是，通过论文的查阅找到了，rabbit算法的内容：[6]

Rabbit密码的加密算法还是比较复杂的，不过通过搜索引擎找到了破解Rabbit密码的现成脚本

点开题目描述：

题目描述

一如既往没有什么卵用的题目描述

下载附件，查看附件内容：

附件内容

附件内容里面是一组密文：

U2FsdGVkX1/+ydnDPowGbjjJXhZxm2MP2AgI

这里使用在线解密工具进行解密：https://www.sojson.com/encrypt_rabbit.html

（本菜鸡不会写，嘤嘤嘤）

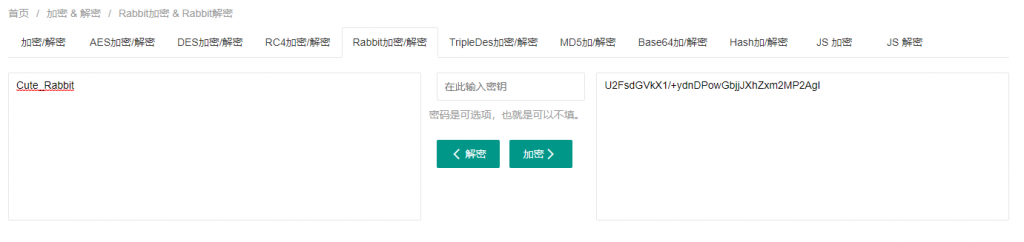解密页面

得到了一个明文：Cute_Rabbit

对得到的明文进行简单的修饰：flag{Cute_Rabbit}

故flag是flag{Cute_Rabbit}

本题主要考察Rabbit流密码加密，简单题

篱笆墙的影子

看到题目，这题应该是考察栅栏密码。（篱笆墙也只能联想到栅栏密码了）

栅栏密码的详细介绍，在上一篇XCTF CRYPTO的WP中有提到，具体内容可以访问上一篇：

XCTF-CRYPTO-新手区 writeup

点开题目描述

题目描述

题目描述就是在说，还是熟悉的味道，唔~。然而也没什么卵用

下载附件，并查看附件内容：

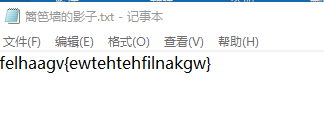
附件内容

附件里面的文件中是一段熟悉密文：felhaagv{ewtehtehfilnakgw}

由于不确定是W型还是传统型，直接使用之前写的两个脚本都跑一下：

传统型栅栏密码

fhetlehhafaiglvn{aekwgtwe}
feiewlltnheaahkatggewvh}{f
fvtae{eklehghwfwati}aelghn
fgeiwevhl}l{tnheeaawhkatfg
fawen}egthalvefkh{higaetlw
fa{ehnweaehfa}lgwtikhvtelg
fa{ehnweaehfa}lgwtikhvtelg
fhgeeeiaweavwhhlk}la{ttfng
fhgeeeiaweavwhhlk}la{ttfng
fhgeeeiaweavwhhlk}la{ttfng
fhgeeeiaweavwhhlk}la{ttfng
flag{wethinkwehavetheflag}
flag{wethinkwehavetheflag}
flag{wethinkwehavetheflag}
flag{wethinkwehavetheflag}
flag{wethinkwehavetheflag}
flag{wethinkwehavetheflag}
flag{wethinkwehavetheflag}

W型栅栏密码

fhetlehhafaiglvn{aekwgtwe}
fvn{eeawltkehhgtaewhaf}igl
fatkegevhgf{leiwlwhtn}aeah
fatfgieaeghlwntvl{ea}khehw
fh{higlteaeawenwahtglvefk}
fh{ehnwafheaeawtik}gletglv
fla{ehnwafhegheavwtik}glet
fla{ttfnwaieeegheavwhhlk}g
fla{ttfng}waieeegheavwhhlk
fla{ttflag}wknieeegheavwhh
fla{theflag}wknihteegheavw
flavetheflag}wknihtew{ghea
fehavetheflag}wknihtew{gal
felhavetheflag}wknihtew{ga
felhaavetheflag}wknihtew{g
felhaagvetheflag}wknihtew{
felhaagv{etheflag}wknihtew
felhaagv{ewtheflag}wknihte

在跑出来的数据中寻找有关flag的相关信息，经查找发现flag数据是：flag{wethinkwehavetheflag}

故本题的flag就是flag{wethinkwehavetheflag}

题目主要考察栅栏密码，签到题。

本题的解题脚本代码还是扔出来一下吧：

def decrype(cipher,key):
    cipher_len = len(cipher)
    if cipher_len%key == 0:
        key = cipher_len / key
    else:
        key = cipher_len / key + 1
    result = {x:'' for x in range(key)}
    for i in range(cipher_len):
        a = i%key;
        result.update({a:result[a]+cipher[i]})
    plainer=""
    for i in range(key):
        plainer = plainer + result[i]
    print plainer

cipher="felhaagv{ewtehtehfilnakgw}"
for n in range(2,20):
    decrype(cipher,n)

RSA

看题目应该是主要考察RSA非对称加密算法的问题，密码学核心考察的问题。

RSA加密算法的详细介绍，在上一篇XCTF CRYPTO的WP中有提到，具体内容可以访问上一篇：

XCTF-CRYPTO-新手区 writeup

点开题目描述：

题目描述

没有太多有用的信息，一如既往

下载附件，并查看附件：

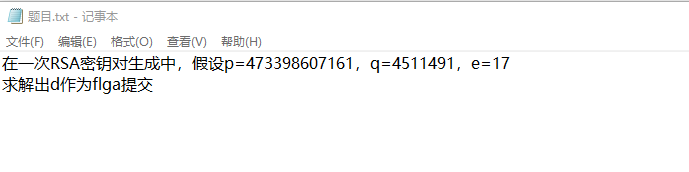题目描述

应该是比较简单的RSA题目，这里就是求解一下逆元。

这里写一个脚本进行求解：（使用到了gmpy2库）

import gmpy2

p = 473398607161
q = 4511491
n = p*q
e = 17

ni = 0
if(gmpy2.is_prime(n)):
    ni = n-1
else:
    ni = (p-1)*(q-1)

d = gmpy2.invert(e,ni)
print(d)

执行脚本，得到运算出的d：125631357777427553

故flag是flag{125631357777427553}

本题主要考察RSA加密算法的简单应用，简单题。

丢失的MD5

这道题目，应该是和MD5相关

点开题目描述：

题目描述

一如既往，没有什么东西

下载附件，查看附件内容：

附件内容

发现是一个python文件，尝试执行一下这个python代码

获得一段数据：e9032994dabac08080091151380478a2

这段数据是不是flag呢？

康一康源代码吧：

import hashlib
for i in range(32,127):
    for j in range(32,127):
        for k in range(32,127):
            m=hashlib.md5()
            m.update('TASC'+chr(i)+'O3RJMV'+chr(j)+'WDJKX'+chr(k)+'ZM')
            des=m.hexdigest()
            if 'e9032' in des and 'da' in des and '911513' in des:
                print des

源代码中找不到有关flag的相关信息，（这题好难呀），那flag很可能就是python的运行结果

尝试加工一下运行数据：flag{e9032994dabac08080091151380478a2}

尝试提交一下flag，发现成功了（这题真简单）

本题考察python2代码的相关知识，签到题。（谁能想到运行结果就是flag呢？）

Alice与Bob

Alice和Bob是密码学中经常使用来进行密码描述的人物名称，所以这道题目可能是加密相关。不过，也推断不出更多的信息。

点开题目描述：

题目描述

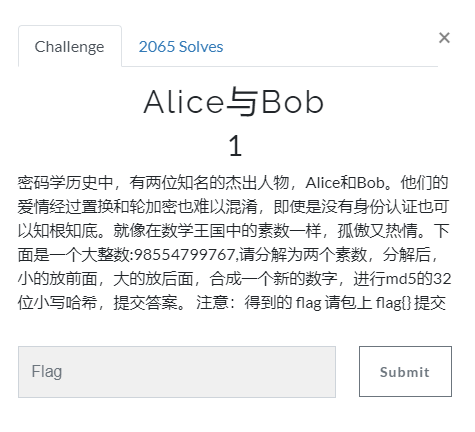
题目描述终于是有用了，看样子，这道题目也是一道签到题目。

将题目描述进行提炼即可解密：

98554799767,请分解为两个素数
分解后，小的放前面，大的放后面，合成一个新的数字
进行md5的32位小写哈希，提交答案
得到的 flag 请包上 flag{} 提交

根据步骤一步一步的来就好

首先需要进行大数分解，这里使用sagemath进行大数分解：

得到两个素数101999和966233

然后进行数字组合，小的放前面，大的放后面，即101999966233

然后进行md5加密，这里写一个简单的脚本进行MD5加密（对脚本的热爱）：

import hashlib
plainer = "101999966233"
m = hashlib.md5()
m.update(plainer)
cipher = m.hexdigest()

print cipher

执行脚本，得到md5加密的结果：d450209323a847c8d01c6be47c81811a

对MD5的加密结果进行修饰：flag{d450209323a847c8d01c6be47c81811a}

故flag就是flag{d450209323a847c8d01c6be47c81811a}

题目主要考察md5加密和大数分解，签到题

rsarsa

看题目应该也是考察RSA加密算法的题目

点开题目描述：

题目描述

没有什么有用的信息，也只是告诉了提交flag的数据格式

下载附件，查看附件内容：

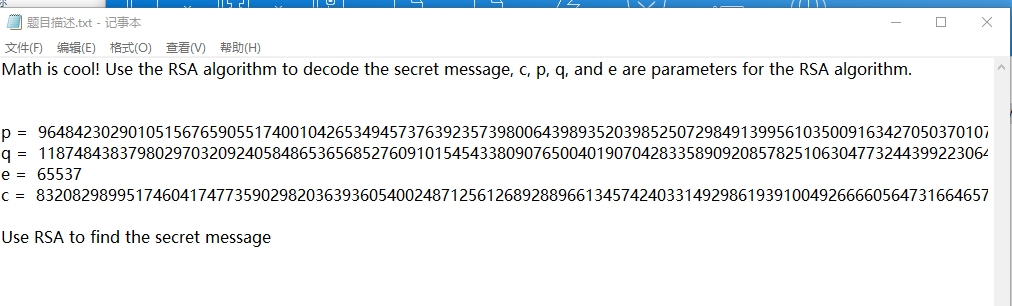
附件内容

应该是RSA数学计算的题目类型

提炼出附件内容中给到的重要数据：

p = 9648423029010515676590551740010426534945737639235739800643989352039852507298491399561035009163427050370107570733633350911691280297777160200625281665378483
q = 11874843837980297032092405848653656852760910154543380907650040190704283358909208578251063047732443992230647903887510065547947313543299303261986053486569407
e = 65537
c = 83208298995174604174773590298203639360540024871256126892889661345742403314929861939100492666605647316646576486526217457006376842280869728581726746401583705899941768214138742259689334840735633553053887641847651173776251820293087212885670180367406807406765923638973161375817392737747832762751690104423869019034

这里使用一个脚本来解决问题：

import gmpy2

p = 9648423029010515676590551740010426534945737639235739800643989352039852507298491399561035009163427050370107570733633350911691280297777160200625281665378483
q = 11874843837980297032092405848653656852760910154543380907650040190704283358909208578251063047732443992230647903887510065547947313543299303261986053486569407
e = 65537
c = 83208298995174604174773590298203639360540024871256126892889661345742403314929861939100492666605647316646576486526217457006376842280869728581726746401583705899941768214138742259689334840735633553053887641847651173776251820293087212885670180367406807406765923638973161375817392737747832762751690104423869019034

n = p*q
if(gmpy2.is_prime(n)):
    ni = n -1
else:
    ni = (p-1)*(q-1)

d = gmpy2.invert(e,ni)
m = pow(c,d,n)

print(m)

运行一下脚本，得到数据：5577446633554466577768879988

对得到的数据进行修饰：flag{5577446633554466577768879988}

故flag就是flag{5577446633554466577768879988}

本题主要考察RSA加密算法相关知识，简单题

大帝的密码武器

看到题目，感觉有点意思，但是暂时联想不到有用的信息

点开题目描述：

一如既往，题目描述不能给到太多的信息，仅仅只给到了提交flag的数据格式

下载附件：

附件

附件是个zip文件，无法打开，尝试修改文件扩展名为zip：

打开zip文件：

发现有两个文件，依次打开两个文件：

附件内容

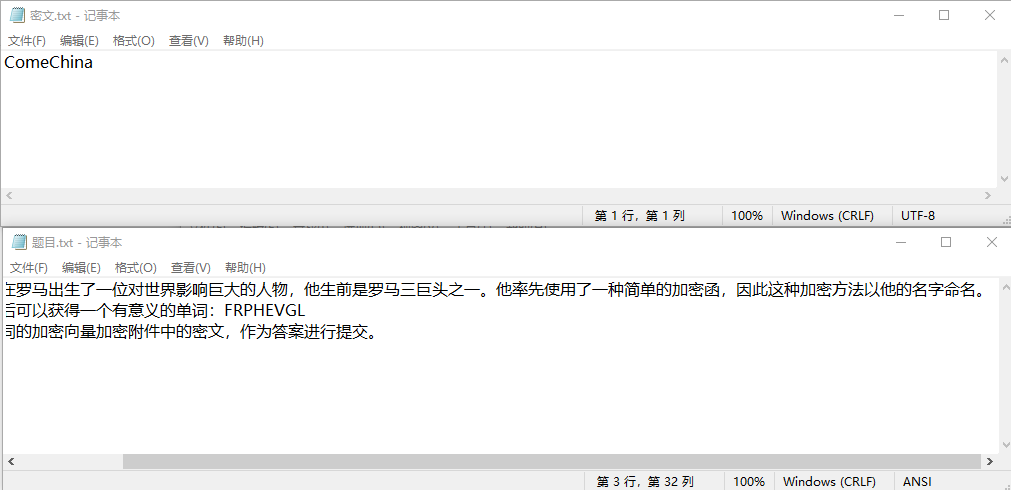
一个题目tip信息，一个需要进行解密的密文

题目tip如下：

公元前一百年，在罗马出生了一位对世界影响巨大的人物，他生前是罗马三巨头之一。他率先使用了一种简单的加密函，因此这种加密方法以他的名字命名。
 以下密文被解开后可以获得一个有意义的单词：FRPHEVGL
 你可以用这个相同的加密向量加密附件中的密文，作为答案进行提交。

根据描述，罗马三巨头应该自然而然就联想到了凯撒加密。

这里先使用一个脚本解决位移向量问题：

dict_list = []
for i in range(26):
    dict_list.append(chr(ord('a')+i))

cipher = "FRPHEVGL".lower()

for n in range(26):
    plainer = ""
    for i in cipher:
        if i in dict_list:
            plainer += dict_list[(dict_list.index(i)-n)%26]
        else:
            plainer += i

    print(plainer+" index:"+str(n))

执行脚本，得到数据：

frphevgl index:0
eqogdufk index:1
dpnfctej index:2
comebsdi index:3
bnldarch index:4
amkczqbg index:5
zljbypaf index:6
ykiaxoze index:7
xjhzwnyd index:8
wigyvmxc index:9
vhfxulwb index:10
ugewtkva index:11
tfdvsjuz index:12
security index:13
rdbtqhsx index:14
qcaspgrw index:15
pbzrofqv index:16
oayqnepu index:17
nzxpmdot index:18
mywolcns index:19
lxvnkbmr index:20
kwumjalq index:21
jvtlizkp index:22
iuskhyjo index:23
htrjgxin index:24
gsqifwhm index:25

发现位移13是一个有意义的单词：security index:13

再写一个小脚本求解密文：

cipher = "ComeChina".lower()
def caesar(n,cipher):
    dict_list = []
    for i in range(26):
        dict_list.append(chr(ord('a')+i))
    plainer = ""
    for i in cipher:
        if i in dict_list:
            plainer += dict_list[(dict_list.index(i)-n)%26]
        else:
            plainer += i

    return plainer

print caesar(13,cipher)

执行脚本，获得数据：pbzrpuvan

对得到的数据进行修饰：flag{pbzrpuvan}

故flag就是flag{pbzrpuvan}

本题主要考察Caesar加密的相关知识，简单题

Windows系统密码

Windows系统密码，根据本菜鸡的知识Windows密码也是使用hash的方式进行加密的，所以本题应该也是在考察hash密码的破解。

点开题目描述：

题目描述

一如既往，没有什么有用的信息

下载附件，查看附件内容：

附件内容

附件给出了4对哈希值：

Administrator:500:aad3b435b51404eeaad3b435b51404ee:31d6cfe0d16ae931b73c59d7e0c089c0:::
 ctf:1002:06af9108f2e1fecf144e2e8adef09efd:a7fcb22a88038f35a8f39d503e7f0062:::
 Guest:501:aad3b435b51404eeaad3b435b51404ee:31d6cfe0d16ae931b73c59d7e0c089c0:::
 SUPPORT_388945a0:1001:aad3b435b51404eeaad3b435b51404ee:bef14eee40dffbc345eeb3f58e290d56:::

这里解密去cmd5网站进行解密，经过反复尝试发现只有

a7fcb22a88038f35a8f39d503e7f0062可以解密出hash数值：

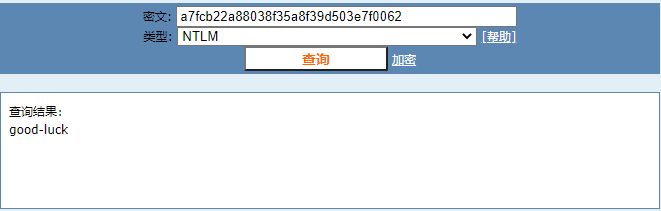
hash解密结果就是：good-luck

对hash解密结果进行修饰：flag{good-luck}

故flag就是flag{good-luck}

本题主要考察Windows系统的数据加密方式，简单题

参考

MD5-维基百科
百分号编码-维基百科
社会工程学-维基百科
流密码-维基百科
Rabbit流密码
[张振广,胡予濮,王璐.流密码Rabbit的安全性分析J].计算机科学,2011,38(02):100-102.

BUUCTF前面的题目偏向简单题目和签到题目，大多数都在考察古典密码，对称密码的相关知识。

本期wp分享到此为止，有时间再来喝杯茶呀！